O objetivo dessa disciplina é fomentar o uso da análise gráfica com o uso do software R. Não será dado enfoque em técnicas quantitativas de análise de dados, mas, em alguns momentos essa associação é de certa forma indispensável.
Além das técnicas gráficas usuais, pretende-se incentivar o uso de alternativas de análise e interpretação de dados estatíticos. O R, pelas suas características de programação, permite que sejam criados vários tipos de análise gráfica, seja uma nova metodologia ou uma combinação de metodologias já existentes.
Por fim, pretende-se que o aluno desenvolva a capacidade de utilizar metodologias gráficas para análise de dados estatísticos utilizando o software R.
|
Sumário |
_________________________________________________________________________________
Para gerenciar os materiais produzidos durante o curso, sugere-se que cada aluno crie um diretório dentro da sua área de trabalho:
$ mkdir ce231
$ cd ce231 $ R |
Assim, todas as tarefas realizadas com o R ficará armazenadas nesse diretório. Toda vez que iniciar um sessão de trabalho, entre nesse diretório, e abra o R.
Não se esqueça de, ao final, salvar sua sessão de trabalho.
> q()
Save workspace image? [y/n/c]: y |
Se você possui algum conhecimento sobre o Emacs é recomendável utilizá-lo durante a utilização do conteúdo desse material. Além de agilizar alguns comandos é possíel fazer comentários e modificar funções gráficas mais facilmente.
No caso de utilizar o sistema operacional Windows, você pode utilizar um script de forma semelhante ao Emacs.
No R existem pacotes gráficos (packages) que geram os gráficos propriamente ditos e, além disso, existem diversos outros pacotes que possuem funções gráficas específicas. Existem ainda, os sistemas gráficos que implementam outras funcionalidades aos gráficos gerados pelos diferentes pacotes. Ainda, esses sistemas permitem integrar os pacotes gráficos, através de funções no pacote grDevices, possibilitando uma maior versatilidade de trabalho com cores e tipos de fontes, por exemplo.
No R existem três tipos de funções gráficas:
Existem muitos pacotes que trabalham com funcionalidades gráficas no R. Por isso, antes de tentar criar algo novo, faça uma busca detalhada no site do R, principalemnte nas listas de emails do site do R e na internet.
As funções de alto nível podem ser aplicadas através do comando par() ou como argumentos em funções gráficas como plot(), por exemplo. Experimente ver quais são as opções da função par(). Para isso, digite o seguinte comando no R:
Aparecerá no arquivo de ajuda, uma lista das opções que podem ser utilizadas, os possíveis valores de cada uma e, no final, alguns exemplos de aplicação. Na tabela 1.1, são apresentadas algumas dessas funções. Experimente aplicá-las em um gráfico!
Antes de iniciar com um exemplo, é recomendável ’salvar’ a configuração original da função par().
Para restaurar a função original, após ter experimentado os comandos da tabela 1.1, basta utilizar
|
|
Como sugestão, tente aplicar as opções da função par() no gráfico:
Para ver quais são os parâmetros atuais, definidos pela função par(), digite o seguinte:
As mudanças efetuadas através da função par() permanecem inalteradas até que outra mudança seja efetuada nessa função. Ou seja, para qualquer gráfico gerado a partir de uma nova configuração da função par(), todos terão as mesmas características. Se a mudança for efetuada através da função plot(), por exemplo, essa mudança será temporária e não afetará novos gráficos.
As funções de “baixo nível”, ao contrário da anterior, podem ser modificadas apenas através da função par(). Estas funções são listadas na tabela 1.2.
|
|
Ainda existem outras funções de ‘baixo nível’ que tratam de margens e localização de figuras dentro da região do gráfico que serão tratadas mais adiante.
Experimente utilizar alguns dos exemplos a seguir, para treinar o uso de algumas funções da tabela 1.2:
A função text() é utilizada aqui para adicionar um texto no gráfico.
Consulte outras opções da função par() e experimente alterá-las no gráfico anterior!
Os gráficos gerados no R podem ser salvos em diferentes formatos de arquivo: postscript, pdf, pictex (LATEX), xfig, bitmap, png e jpeg e exclusivamente no Windows, win.metafile e bmp.
No R, uma ’saída’ gráfica é direcionada para um dispositivo em particular, que gerencia o formato do arquivo que será criado. Assim, quando deseja-se que uma saída gráfica seja salva, deve-se abrir um dispositivo gráfico, para receber essa saida, e depois esse dispositivo deve ser fechado.
Veja o seguinte exemplo para gerar um simples gráfico no formato postcript:
As funções lines(), points() e text() permitem inserir, em um gráfico, linhas, pontos e texto, respectivamente. Para saber quais opções podem ser utilizadas, utilize a opção de ajuda de cada uma das funções.
Os dois principais comandos relacionados com linhas são lty e lwd. O primeiro controla o tipo de linha: sólida, pontilhada. O segundo, controla a largura da linha.
A largura da linha é especificada por um número, por exemplo lwd=2. Esse valor varia com o tipo de dispositivo empregado para visualização. Na tela de um monitor, o número 1, por exemplo, representa um pixel. Veja alguns exemplos a seguir.
No R é possível, além de utilizar os formatos pré-definidos de linhas em lty, utilizar versões ’pessoais’. Esse formatos devem ser fornecidos como strings (entre aspas). Um número ímpar especifica o comprimento da linha e um número par especifica o tamanho do espaço vazio (gap).
No R pode-se adicionar diferentes tipos de pontos em gráfico. Basta definir qual símbolo deve ser utilizado entre os 26 disponíveis. Utiliza-se a função points(). Ainda, é possível utilizar caracteres como síbolos. Simplesmente, defina o símbolo entre aspas.
Experimente utilizar a função show.pch() do pacote Hmisc,
Com a função text(), pode-se inserir textos no gráfico. Nessa função deve-se informar a posição do texto, fornecendo as coordenadas em relação à região do gráfico. Uma opção útil nessa função é adj, que indica a justificação do texto. Nessa opção, 0 significa um alinhamento à esquerda, 0.5 centrado e 1 justificado à direita. Ainda, na opçãp adj, pode-se fornecer a informação da forma c(hjust,vjust), onde hjust indica o alinhamento horizontal e vjust um alinhamento vertical. Veja alguns exemplos:
Quando um texto é muito longo ou deseja-se fazer a quebra de uma linha, deve-se utilizar a opção ‘\n’ no ponto de quebra de uma linha.
Estes comandos são utilizados depois que os gráficos são criados.
Experimente usar o exemplo seguinte. Gere o gráfico e depois, na janela gráfica, selecione um ponto com o ’mouse’ (dê um ’clique’ dentro do gráfico). Nesse momento, aparecerá na janela do R as coordenadas do ponto.
Agora, utilize o mesmo gráfico, definindo a opção com n = 2 e type=‘l’.
Com o ’mouse’, selecione dois pontos dentro do gráfico.
Experimente, também, utilizar outras opções para type (veja help(locator)).
A função locator(), também, pode ser utilizada em associação com a função points().
e com a função text(),
Da maneira a seguir, você deve clicar duas vezes no gráfico.
Para cancelar o processo antes de localizar todos os pontos, aperte o botão direito do ’mouse’. No Windows, apertando o botão direito é mostrada a opção ’stop’.
Cuidado! Se a janela gráfica for alterada antes que a total identificação dos pontos seja feita, os pontos desaparecem.
Utiliza-se a função identify() para dar nomes aos pontos de um gráfico. Para utilizar essa função são necessárias as coordenadas (x,y) e um vetor com nomes dos pontos (string):
Como exemplo, considere o seguinte conjunto de dados e o respectivo gráfico:
Para identificar cada ponto no gráfico, utilize a função identify() da seguinte maneira:
Agora, clique próximo aos pontos para poder identificar cada um deles. Caso não deseje identificar todos, aperte o botão direito do ’mouse’.
Se o ponteiro do ’mouse’ ficar muito distante do ponto, aparecerá uma mensagem de aviso no R. Continue ’clicando’ até conseguir se aproximar do ponto desejado.
Existem, basicamente, três maneiras de definir cores nos gráficos. Pode-se utilizar os comandos fg, bg e col. A função col possui variações, podendo ser aplicada em várias situações, como mudança de cor de eixos, títulos etc, como visto na tabela 1.1.
Dependendo do local onde a função col é utilizada, ela pode funcionar de diferentes maneiras. Por exemplo, dentro da função plot() ela pode ser utilizada para colorir símbolos, texto, linhas. Já, dentro da função barplot() ela é utilizada para colorir as barras.
A função fg é utilizada para colorir eixos e bordas. Observe que, essa opção pode causar alguma sobreposição de cores se utilizada junto com comandos específicos de cores para eixos e texto do tipo col.axis, col.main.
A função bg é utilizada para controlar a cor de fundo de um gráfico.
Para especificar uma cor, pode-se utilizar números ou strings (nome da cor). Por exemplo, ’blue’ indica que a cor azul foi definida. No R existem 657 nomes de cores para serem utilizados. Experimente a opção colors() para ver os nomes de cores disponíveis. A função palette() também fornece alguns nomes de cores.
Experimente utilizar a seguinte função do pacote Hmisc:
A função rgb() permite que sejam especificadas cores como uma combinação de VERMELHO-VERDE-AZUL (Red,Green,Blue). por exemplo, a cor vermelha é especificada como rgb(1,0,0).
Se você quer saber qual são os números que devem ser fornecidos para uma determinada cor, utilize a função col2rgb(). Veja o exemplo a seguir:
Os valores da função rgb() também podem ser fornecidos na forma de um string #RRGGBB, em que cada par corresponde a um numero de 0 a 255(FF).
A função rgb() possui uma opção maxColorValue que define a amplitude de variação dos números.
Veja o exemplo, a seguir, para ver como utilizar cores com rgb (aproveite para conhecer a função rect()):
Existem ainda alguns conjuntos de cores já definidos no R. Esses conjuntos formam alguns padrões que podem ser utilizados em diferentes tipos de gráficos. Esses padrões, em geral, são utilizados em gráficos que necessitam de mais de uma cor para ser aplicada.
|
|
Dentro dos parênteses, são inseridas opções, em geral, o número de cores. Experimente o seguinte exemplo no R:
Observe que, a cor final pode depender da resolução do vídeo, do tipo de impressora, tipo de papel além de outras condições. Todas as cores geradas, são armazenadass pelo R como cores do tipo rgb().
Veja alguns exemplos de cores na função de demonstração graphics:
Experimente ainda, utilizar essa função para entender um pouco mais sobre cores
Nessa seção, veremos como construir mais linhas, com os comandos segments() e abline, além de flechas (arrows).
A sintaxe da função segments() é a seguinte:
x e y representam as coordenadas dos pontos que devem ser unidos. No exemplo, a seguir, pode-se colocar em um gráfico várias linhasbaseadas na função segments().
Experimente alterar opções da função segments() e gere outras figuras!
De forma muito semelhante a função segments(), a função arrows() permite que sejam feitas setas dentro de um gráfico. Entre os argumentos, code (0 a 3) indica em que lada a ponta da flecha vai estar, angle indica o ângulo da flecha e length indica o tamanho da flecha. Outras opções como tipo e cor da linha também são aceitas.
A função arrows() pode ser utilizada da seguinte maneira (firura 1.3):
A função abline() é utilizada, em geral, para representar coeficientes de um modelo, mas, pode ser utilizada para gerar uma linha em um gráfico. A idéia é utilizar os coeficientes de um modelo, em geral de uma regressão linear simples para gerar uma reta no gráfico. Mas, pode-se utilizar um simples argumento para gerar uma linha vertical ou horizontal. Veja os exemplos a seguir:
Primeiro, geramos um gráfico de dispersão entre x e y.
Em seguida, pode-se construir um modelo para representar a relação entre x e y. Nesse caso, um modelo de regressão linear simples (uma reta):
Existem pelo menos três maneiras de inserir uma reta no gráfico. No caso de uma regressão linear simples, pode-se inserir o objeto do tipo lm, ‘chamar’ os coeficientes do modelo ou simplesmente digitando os números correspondentes aos coeficientes.
Ainda, pode-se inserir, com o comando abline() uma reta horizontal e ou uma reta vertical.
Algumas figuras geométricas podem ser geradas através de algumas funções no R. Nesta seção trataremos de algumas destas funções que podem auxiliar na criação de gráficos.
A primeira delas é a função rect() que pode ser utilizada para gerar retângulos. A sintaxe da função é a seguinte:
onde xleft, ybottom, xright, ytop são as coordenadas do retângulo dentro da região do gráfico, density e angle são argumentos que definem a existência ou não de linhas dentro do retângulo e o ângulo de inclinação das linhas, respectivamente.
Outras opções fazem parte da configuração de cor, tipo de linha etc.
Veja o exemplo da figura 1.2.3 para saber como trabalhar com a função rect(). Faça alterações nos argumentos da função para entender como ela funciona.
Experimente também, utilizar o exemplo disponível no documento de ajuda sobre a função no R.
Em muitas situações, podemos estar interessados em construir um polígono, ou seja, unir diferentes pontos em um gráfico. A função polygon permite esse tipo de tarefa.
Duas novas funções aparecem nos comandos da figura 1.5.
A primeira é a função box(). Essa função cria uma ‘caixa’ ao redor da região do gráfico (questões sobre dimensão e margens serão estudadas mais adiante).
A segunda é a função chull(), que retira do conjunto de coordenadas os pontos extremos de forma a contornar toda a extensão periférica dos pontos. Observe que, o objeto perif contém os pontos que formam essa região e x[perif] e y[perif] contém as coordenadas desses pontos.
Nesse caso, a função polygon() simplesmente faz a união desses pontos através de uma linha.
Um aplicação pode ser com o uso da distribuição Normal.
Lembre-se que a função dnorm() gera os valoes de uma distribuição Normal padrão. Nesse caso, a função polygon() utiliza a informação sobre a distribuição para poder acompanhar a linha da curva da distribuição Normal.
Como sugestão, tente implementar outras opções para símbolos e ainda, abra o arquivo de ajuda dessa função para ver mais exemplos.
Esta função pode ser utilizada para construir círculos, quadrados, entre outros desenhos. Nesse momento, vamos trabalhar apenas com círculos. Se tiver mais interesse, consulte a documentação de ajuda dessa função.
Observe nos argumentos da função, que existem muitas opções:
x e y fornecem as coordenadas do centro do símbolo e circles define o símbolo do tipo círculo. Observe a diferença entre as figuras 1.7 e areffig:simbolo2. Na figura 1.7 a opção inches foi definida como TRUE. Isso faz com que o tamanho dos círculos seja relacionado a escala em polegadas. Já, quando a opção é FALSE, a escala está relacionada com o eixo x. Veja os exemplos nas figuras 1.7 e 1.8:
Observe nas linhas de comando que a opção add foi definida como TRUE. Esta opção indica que os novos símbolos devem ser adicionados ao gráfico. Experimente utilizar a opção FALSE para ver o resultado.
Toda vez que um dispositivo gráfico é aberto no R, ele é dividido em três regiões: margem externa, a região da figura ativa e a região do gráfico ativo (figura 1.9).
No caso de existirem múltilos gráficos, as regiões ficam caracterizadas conforme a figura 1.10
O tamanho dessas regiões é controlado pela função par().
Por ‘default’ não há margens externas quando da geração de um gráfico. As margens externas podem ser inseridas de três maneiras:
Experimente alterar as opções gráficas da função par(), como no exemplo da figura 1.11.
Nesse caso, você deverá perceber mudanças no dispositivo gráfico. Experimente alterar as opções do parâmetro oma.
O R determina a região da figura considerando as dimensões das margens externas e do número de figuras no dispositivo gráfico. A região da figura pode ser determinada pelo comando fig especificando left, right, bottom, top. Nesse caso, cada valor é uma proporção da figura desconsiderando os valores das margens externas. O comando fin especifica a largura e altura, width, height da região da figura em polegadas e faz a centralização da região da figura no gráfico.
As margens da região da figura podem ser controladas utilizando o comando mar. Esse comando também utiliza a ordem bottom, left, top, right. Cada valor representa o número de linhas de texto. Os números default são c(5,4,4,2) +0.1. Da mesma forma como em outros comandos, pode-se determinar o tamanho das margens em termos de polegadas utilizando o comando mai.
A região do gráfico é determinda pela diferença entre a região da figura e a região das margens da figura. As dimensões podem ser controladas pelo comando plt, fornecendo as especificações da forma left, right, bottom, top. Pode-se ainda definir as dimensões, width, height, em termos de polegadas (inches). Ainda, existe o comando pty que controla o quanto do espaço disponível que a regiã oda figura deve ocupar. O valor padrão é ’m’, que indica que todo o espaço disponível deve ser ocupado. Pode-se utilizar a opção ’s’ que indica que a região do gráfico deve ocupar o espaço disponível (região da figura menos a região das margens), mas, esse espaço deve ser um quadrado.
Quando um gráfico é gerado, o R irá colocar o resultado (output) na ’região do gráfico’. Qualquer resultado que seja gerado fora das coordenadas da região do gráfico não aparecerá. Mas, existem alguns mecanismos que permitem que se insiram informações fora da região do gráfico (clipping). Por exemplo, pode ser necessário inserir uma legenda em uma posição fora das delimitadas pelas dimensões da região do gráfico.
A opção xpd controla a ’permissão’ para inserir informações além da região do gráfico. Para xpd=NA, é permitido inserir informações em toda a região do dispositivo gráfico. Já, para uma opção xpd=TRUE, é permitido utilizar a região da figura e para a região do gráfico, somente, utiliza-se a opção xpd=FALSE, que é, por sua vez, o valor padrão.
Para saber quais as dimensões da janela gráfica, basta digitar
Para alterar, pode-se utilizar, por exemplo:
O comando mfrow ou mfcol permitiam inserir vários gráficos em um mesmo dispositivo. Mas, todos ocupavam as mesmas dimensões.
Nessa sessão, veremos como utilizar a função layout(). Basicamente, essa função permite inserir vários gráficos com dimensões diferentes.
Para utilizar essa função é necessário fornecer uma matriz especificando o número de posições que serão utilizadas. No exemplo, a seguir, deverão ser gerados quatro gráficos sobre a janela gráfica.
Observe que nesse caso, todos os espaços terão o mesmo tamanho. Mas, é possível definir tamanhos diferentes para cda gráfico. A opção heights ou widths podem ser utilizadas para definir esses tamanhos.
Nesse caso, o gráfico superior ocupa dois terços do espaço disponível (2∕(2 + 1)), enquanto que o gráfico inferior ocupa um terço do espaço disponível (1∕(2 + 1)).
Ainda, a altura das linhas, nesse exemplo, funciona de forma independente das colunas. Para forçar que as colunas também tenham o mesmo formato das linhas, utiliza-se a opção respect=TRUE. Veja o que acontece com o seguinte exemplo:
Pode-se, ainda, definir dimensões em centímetros, utilizando a função lcm. O exemplo a seguir, mostra os gráficos separados 0,5 cm.
Assim como matrix(), pode-se utilizar as funções rbind() ou cbind().
Experimente gerar outras configurações de gráficos utilizando a função layout().
Ainda é possível utilizar a função layout.show() para ver como está dividida a janela gráfica.
A função text() permite inserir texto dentro da região do gráfico. Para inserir um texto na região da figura ou nas margens, utiliza-se a função mtext(). O argumento outer permite definir onde o texto será inserido. O argumento side informa em qual margem: 1-abaixo; 2-esquerda; 3-acima; 4-direita.
O texto é inserido em número de linhas, na região da figura 1.13 ou nas margens externas 1.14, podem ser definidas as coordenadas pelo usuário.
Veja o exemplo 1.15 para ver como utilizar a função mtext(). Nesse caso, quando você tenta inserir um texto com a função text() aparece uma BF mensagem de erro, pois a posição requerida fica na região da figura e não do gráfico. Por isso, a função mtext() deve ser utilizada nessa situação. Experimente ver os argumentos da função mtext() e tentar novas opções.
Já vimos alguns comandos sobre eixos quando estudamos funções de alto nível. Nessa seção veremos como trabalhar com o comando mgp. Esse comando controla a distância de alguns componentes dos eixos em relação a borda da região do gráfico.
Como valor padrão, o comando mgp tem o valor c(3,1,0). Os comandos xaxs e yaxs controlam o estilo dos eixos de um gráfico. As opções correntemente implementadas são i e r. Experimente mudar algumas opções no exemplo a seguir.
Ainda, pode-se alterar as marcações de escala dos eixos com o comando tcl. tcl especifica o tamanho da marca como uma fração do tamanho da linha de texto. Alterando o sinal, muda-se o sentido da marcação.
Em algumas situações, podemos estar interessados na geração de vários gráficos em diferentes janelas gráficas. No R, existem algumas funções que auxiliam no controle dessas janelas gráficas.
Para abrir uma nova janela gráfica, pode-se utilizar, no Windows, x11() ou window(). No Linux, utilize X11(). Experimente abrir várias janelas gráficas ao mesmo tempo. Observe que em cada janela, na parte superior, aparece o número da janela e se ela está ativa ou não.
Para movimentar-se entre as janelas, você pode utilizar dev.set(). Entre parênteses, insira o número da janela gráfica que você quer trabalhar. Ainda, você pode utilizar dev.next() para saber qual a próxima ou dev.prev() para saber qual o número da janela anterior (considerando a ordem de abertura das janelas).
O comando dev.off() fecha a janela gráfica.
Em alguns gráficos, pode-se ter a necessidade de se inserir fórmulas matemáticas. No R, pode-se utilizar tanto o formato de texto quanto expressões que gerem um resultado de interesse. A função expression(), pode ’desenhar’ símbolos que poderão ser utilizados em gráficos.
Utilize a demo(plotmath) ou help(plotmath) para saber quais expressões podem ser utilizadas em um gráfico no R. Após, tente reproduzir as expressões contidas na figura 1.16:
Já utilizamos a função plot() para construir alguns gráficos simples. Nessa seção, vamos explorar um pouco mais os argumentos dessa função. Acompanhe na seqüência, a seguir, alguns dos principais argumentos da função plot().
Como inserir títulos:
Como mudar o tamanho dos títulos:
Como alterar cores:
Como trabalhar com as "marcas de eixos":
Como trabalhar com eixos:
Como controlar a exibição de eixos:
Como controlar os limites de eixos:
Ainda, com relação ao tipo de gráfico, podem ser definidas as seguintes opções:
Outro tópico bastante usual em gráficos é a inserção de legendas em um gráfico.
Considere o seguinte conjunto de dados para iniciar o trabalho:
Um simples legenda pode ser inserida com o comando legend(). Deve-se inserir as coordenadas, o texto da legenda e o tipo de caracter:
Pode-se utilizar os nomes dos objetos:
O comando fill pode ser utilizado para preencher os símbolos:
Se você tiver linhas, pode-se representá-las da seguinte forma (uma opção):
A posição da legenda também pode ser determinada por comandos, ao invés de coordenadas (figura 1.17):
|
> plot(x, y, type = "n") > legend("bottomright", "(x,y)", pch = 1, title = "bottomright") > legend("bottom", "(x,y)", pch = 1, title = "bottom") > legend("bottomleft", "(x,y)", pch = 1, title = "bottomleft") > legend("left", "(x,y)", pch = 1, title = "left") > legend("topleft", "(x,y)", pch = 1, title = "topleft, inset = .05", + inset = 0.05) > legend("top", "(x,y)", pch = 1, title = "top") > legend("topright", "(x,y)", pch = 1, title = "topright, inset = .02", + inset = 0.02) > legend("right", "(x,y)", pch = 1, title = "right") > legend("center", "(x,y)", pch = 1, title = "center")
|
Veja outros exemplos e opções no help da função legend().
Tente reproduzir as figuras a seguir, utilizando comandos básicos do R. Em cada figura são listadas as principais funções utilizadas em cada uma delas.
Obviamente, a reprodução não precisa ser perfeita (considerando, principalmente, dimensões e cores) mas, você deve tentar aproximar ao máximo cada componente do gráfico.
> plot(1:10, 1:10, type = "n", ann = FALSE, axes = TRUE, bg = "green", + xaxt = "n", yaxt = "n") > texto <- substring("preciso", 1:7, 1:7) > text(seq(1.7, 2.9, by = 0.2), rep(2, 7), texto, col = rainbow(7), + cex = 2.5) > text(5, 5, "treinar", srt = 45, cex = 2.5) > segments(1, 7.6, 3, 7.6, lty = 3, lwd = 5) > text(2, 8, "gráficos", cex = 2) > text(8, 8, "no") > rect(7.5, 7.5, 8.5, 8.5) > text(8, 5, "R", font = 4, cex = 4, col = "blue") > arrows(2.5, 2.5, 4.5, 4.5, srt = 45, code = 2, lty = 2) > arrows(4.5, 5, 2.5, 7.5, srt = 90, code = 2, lty = 1, lwd = 3) > arrows(3, 8, 7.5, 7.5, srt = 0, code = 2, lty = 1, angle = 10, + len = 0.4) > arrows(8, 7.5, 8, 5.5, srt = -90, code = 2, lty = 2, len = 0.9, + angle = 60) > text(8, 2, "Eu vou\n conseguir!", cex = 2, col = "red") > points(seq(7, 9, len = 10), rep(4, 10), pch = "*", col = "violet", + cex = 1.5)
|
> plot(1:10, 1:10, type = "n", ann = FALSE, axes = FALSE, main = "Bandeira do BRASIL") > rect(1, 2, 10, 9, col = "darkgreen") > polygon(c(5.5, 1.2, 5.5, 9.8), c(2.2, 5.5, 8.8, 5.5), col = "yellow") > symbols(5.5, 5.5, 2, bg = rgb(0, 0, 1), add = TRUE) > rect(3.54, 5.3, 7.46, 5.8, col = "white") > text(5.5, 5.5, "ORDEM E PROGRESSO", col = "darkgreen") > points(5.92, 5.98, , pch = 8, col = "white") > points(c(6.06, 5.91, 6.07, 6.13, 6.24, 5.68, 5.29, 5.19, + 5.03, 4.87, 5.13, 5.18, 5.38), c(5.14, 4.82, 4.67, 4.99, + 5.1, 4.9, 4.55, 4.86, 5.06, 5.06, 4.69, 4.47, 4.31), + pch = 8, col = "white") > points(c(5.73, 5.88, 5.51, 5.79, 5.96, 6.08, 5.34, 5.5, 5.23, + 5.12, 5.55, 5.87, 6.04), c(5.01, 4.58, 4.66, 4.84, 5.1, + 4.71, 4.88, 4.56, 4.55, 4.95, 4.42, 4.49, 4.64), pch = 8, + col = "white")
|
> plot(1:10, 1:10, type = "n", ann = FALSE, axes = FALSE) > symbols(5, 5, 2, add = TRUE, inc = FALSE) > symbols(c(4, 6), c(6, 6), c(0.3, 0.3), add = TRUE, inc = FALSE) > points(c(4.041275, 6.086176), c(6.006826, 6.006826), pch = c(44, + 44), cex = 4, col = "blue") > points(c(7.022771, 2.997524), c(4.974744, 5.011604), pch = c(41, + 40), cex = 7) > segments(4.467296, 3.426621, 5.617553, 3.297611, col = "red") > segments(4.22, 7.1, 5.04, 9, 1) > segments(5.04, 9.01, 5.96, 7.02) > symbols(5.16, 8.97, 0.2, add = TRUE, inc = FALSE, bg = "yellow") > points(4.989172, 4.827304, pch = 94, cex = 3) > points(c(3.49, 3.54, 3.84, 4.07), c(4.71, 4.31, 4.21, 4.6), + pch = 42, col = 5:8) > points(c(5.81, 6.05, 6.41, 6.13), c(4.53, 4.01, 4.18, 4.66), + pch = 42, col = 5:8)
|
|
Sumário |
_________________________________________________________________________________
No R existem, além dos pacotes básicos, vários outros pacotes (packages) que geram muitos tipos diferentes de gráficos. Nesta seção, iremos estudar como gerar gráficos estatísticos utilizando estes diferentes pacotes.
Entre na página do R e explore alguns pacotes, claro, dando enfoque para a parte gráfica.
Para ’baixar’ um pacote, no R digite
Também daremos algum enfoque na forma de apresentação de gráficos, procurando seguir as normas de publicação e, claro, dentro dos aspectos estatísticos.
Segunda avaliação: Para a segunda avaliação, cada aluno deverá escolher um pacote do R, obviamente, que trabalhe com funções gráficas. Um das questões será a entrega de um trabalho (um gráfico) baseado em uma ou mais funções gráficas de um pacote. Você deve utilizar somente as funções do pacote e/ou funções básicas do R, ou seja, você deve usar a função require() apenas uma vez. Procure utilizar dados originais ou então, simule-os no próprio R (indique a semente set.seed()).
Após a escolha do pacote, envie uma email para o professor com o subject pacote, informando qual o nome do pacote. A preferência será dada pela ordem de chegada dos emails.
O trabalho deverá ser entregue no dia da segunda avaliação.
Utilize a aula de hoje para pesquisar esses pacotes.
Nesta seção veremos alguns pontos que tratam da apresentação de gráficos, como por exemplo, títulos, formato etc. As informações contidas desta seção são baseadas nas Normas para apresentação de trabalhos científicos publicada pela UFPR. Estas normas, por sua vez, baseiam-se nas normas da ABNT (Associação Brasileira de Normas Técnicas). Mesmo assim, muitas revistas científicas, por exemplo, podem possuir normas ou recomendações diferentes das apresentadas nesse e em outros textos.
Procure, daqui para frente, observar os detalhes de apresentação de gráficos, não só em relação as normas de apresentação, mas também com relação à qualidade de apresentação das informações.
Existem algumas características fundamentais em gráficos que podem gerar diferentes percepções em diferentes indivíduos:
Cada indivíduo possui uma percepção diferente em determinados aspectos.
Dependendo da finalidade, um gráfico pode ser classificado em:
Em um gráfico deve-se procurar observar alguns princípios. Basicamente, um gráfico deve ser:
Inicialmente, um gráfico tem a finalidade de apresentar uma informação de maneira clara, rápida e objetiva, além de resumir, organizar e apresentar dados de qualquer natureza.
Obviamente, existem naturezas diversas, bem como objetivos variados na apresentação de gráficos. Pode-se, por exemplo, citar gráficos com fins promocionais. Muitas vezes, eles não seguem quaisquer normas rígidas de apresentação. Mesmo nesses casos, deve-se ter sempre em mente que a informação não pode ser modificada. Aspectos relacionados com a maneira de evidenciar ou obscurecer informações em gráficos não serão tratados nesse texto.
Elementos básicos:
Assim como tabelas, os gráficos devem ser referenciados no texto. Se eles ocorrem em um trabalho, é porque possuem alguma importância, fornecem alguma informação. Portanto, eles precisam ter alguma explicação ou comentário a respeito deles no corpo do trabalho.
Por esse motivo, os gráficos devem ser numerados seqüencialmente ao longo do texto, independente do tipo. Insere-se, no texto, a palavra Gráfico e em seguida o número. Pode-se abreviar a palavra Gráfico. Em alguns textos ou revistas, podeser exigida a palavra figura.
Exemplo:
GRÁFICO 1 - Número médio mensal de acidentes de trânsito com ciclistas em Curitiba no ano de 2005.
No caso de capítulos, deve-se utilizar a numeração correspondente ao capítulo.
Exemplo: No capítulo 1 use GRÁFICO 1.1
GRÁFICO 1.2
No capítulo 2 use
GRÁFICO 2.1
GRÁFICO 2.2
De maneira simples, o título de um gráfico deve ser suficiente para o leitor entender seu conteúdo e sua inserção no contexto do material publicado.
Basicamente, o título traz uma breve descrição do conteúdo do gráfico e uma data de referência, quando for o caso.
Em gráficos estatísticos, é recomendável que a fonte (responsável) dos dados seja mencionada. Normalmente a fonte é apresentada abaixo do gráfico, com uma tamanho de letra menor do que a do título, iniciada com a expressão Fonte.
Em um gráfico, as informações que possuem uma escala devem ser apresentadas com clareza. Os números da escala devem estar na posição horizontal e na região externa dos eixos. A unidade de medida deve aparecer no final de cada linha do gráfico.
Caso não seja possível apresentar a escala por completo, pode-se fazer um corte no eixo correspondente para informar que a escala não está completa.
Cores: dependem dos recursos e da finalidade. Em geral, para publicação em revistas científicas, em se tratando de gráficos estatísticos, são utilizados apenas gráficos em preto e branco. Uma alternativa é utilizar tonalidades de preto, passando pelo cinza, até o branco.
Além de cores, podem-se utilizar hachuras ou linhas pontilhadas
legenda: Tanto cores, como linhas pontilhadas ou hachuras devem ser referenciadas em uma legenda.
Em geral, pode-se dizer que quando um gráfico não consegue expressar a devida informação sem a necessidade de números, é porque uma tabela deve ser uma opção mais adequada.
Nesta seção, estudaremos alguns gráficos univariados. O principal objetivo destes gráficos é fazer uma análise descritiva de dados. Entende-se por análise descritiva a obtenção de informações que auxiliem na interpretação e na avaliação da qualidade dos dados em determinadas situações. Basicamente a freqüência e a forma de distribuição dos dados são os aspectos que podem ser considerados mais relevantes em uma análise gráfica univariada. Obviamente, em casos particulares, pode-se ter interesses diferentes dos aqui apresentados.
No R, iremos utilizar alguns conjuntos de dados provenientes de pacotes e em algumas situações, utilizaremos funções específicas de alguns pacotes.
O objetivo de um gráfico ramo-e-folhas é resumir os dados de tal forma que se possa ter uma noção da forma da distribuição dos dados (simétrica, assimétrica), a freqüência de observações, vazios entre os dados e possíveis dados discrepantes (outliers).
As observações devem ser divididas em duas partes. A primeira, chamada de ramo, é colocada à direita de uma linha vertical, e a segunda, chamada de folhas, é colocada á esquerda. Por exemplo, se a variável possui valores do tipo 2, 34; 2, 98, o número 2 será o ramo e 34 e 98 serão as folhas.
A maneira como são distribuídos os ramos e folhas podem variar em função da quantidade de dados. Em alguns casos, pode-se ter uma visualização melhor com uma separação dos dados por ramo.
Esse gráfico pode não ser muito útil quando existem muitas observações.
Vamos considerar um conjuto de dados simulados no R:
Para construir o gráfico, utiliza-se a função stem().
Veja os argumentos e o help da da função stem():
Experimente alterar alguns dos parâmetros da função. Tente, também, aumentar o tamanho e o tipo de dado gerado. Por exemplo, gere dados de uma distribuição Normal, utilizando rnorm().
O box-plot é um gráfico que mostra a posição central, dispersão e simetria dos dados de uma amostra , comprimento de caudas e dados discrepantes. É utilizado para resumir as informações de um conjunto de dados.
Esse gráfico é baseado no “resumo dos 5 números"(fivenum()).
Considere o seguinte conjunto de dados: 17, 22, 23, 27, 29, 32, 38, 42, 46, 52, 60, 92
Para construir o box-plot dessas observações, devemos seguir os seguintes passos:
Limite inferior = Q1-36=25-36=-11
Limite superior = Q3+36=49+36=85
No R, basta utilizar a função boxplot() informando a variável que será utilizada.
Além do gráfico, a função boxplot() retorna outras estatística que podem ser de interesse.
Veja outras opções da função boxplot().
Se o objeto que se deseja utilizar a função boxplot() é apenas uma variável numérica, será construído apenas um box-plot. No caso de existir mais de uma variável, por exemplo, um data.frame, a função boxplot() irá construir um box-plot para cada coluna.
Se existir uma variável do tipo factor, pode-se utilizar uma fórmula para construir um box-plot para cada categoria.
Por exemplo, considere os dados sobre gatos (cats) do pacote MASS. Existem três colunas: Sex (sexo), Bwt (peso do corpo), Hwt (peso do coração).
Para construir um box-plot para cada um dos sexos, utiliza-se o seguinte:
Experimente alterar algumas opções da função boxplot(). Veja, por exemplo, como mudar cores.
A opção notch=TRUE insere um corte (entalhe) em cada box-plot. Quando esses cortes se sobrepõem, isso indica que não deve haver diferenças entre as medianas dos grupos.
O gráfico de setores ou circular, também conhecido como ’pizza’ pode ser utilizado para representar a freqüência de observações de diferentes categorias. O tamanho de cada setor é proporcional ao número de observações em cada categoria. O tamanho pode ser definido em números percentuais ou absolutos.
Em geral, um gráfico de setores não é um bom modo de representar dados porque o olho humano tem dificuldades para comparar áreas relativas. em comparação com medidas lineares.
No R, a função utilizada para esse tipo de gráfico é pie().
Vamos utilizar os dados do arquivo cats do pacote MASS:
Experimente obter algumas informações,
A função tapply() (t de table) pode ser utilizada para obter estatísticas por grupos:
Nesse exemplo, utiliza-se a variável resposta Bwt, agrupa-se por Sex e estima-se a média de cada grupo.
Suponha uma nova variável, onde, se o peso do coração for maior ou igual a 9,5, o gato está apto e, caso contrário, estará inapto.
Obtenção de uma soma marginal:
Para obter freqüências relativas, utilize
Se for de interesse obter valores em percentual, multiplique por 100.
Para obter as proporções em função do total geral, basta utilizar
(com duas casas decimais)
O gráfico de setores pode ser obtido da seguinte maneira:
Outros exemplos
Alguns outros exemplos podem ser vistos a seguir. Por exemplo:
Para esses dados, um gráfico de setores pode ser construído da seguinte forma:
Pode-se trabalhar com cores da seguinte forma:
Experimente trabalhar com cores:
Existem outros parâmetros gráficos que podem ser utilizados. Veja os argumentos da função pie() e outros exemplos utilizando ?pie.
Assim como o gráfico de setores, o gráfico de barras é utilizado para representar a freqüência absoluta ou percentual de diferentes categorias.
Basicamente, são construídas barras proporcionais as freqüências. No R, utiliza-se a função barplot(). Como exemplo veja a figura 2.6,
Também, pode-se trabalhar com cores (figura 2.7):
Quando trata-se de dados dispostos em uma tabela, a função barplot() ’enxerga’ os dados da seguinte maneira (figura 2.8):
Para inverter as posições, basta utilizar a função t(), que transpõe a matriz de dados (figura 2.9):
Ainda, pode-se colocar as barras lado a lado e inserir uma legenda (figura 2.10) :
Se os dados estão no formato de uma matriz, as barras são agrupadas para representar os dados de maneira adequada. Por exemplo, considere o seguite conjunto de dados:
Para esses dados, a função barplot() retorna o seguinte gráfico:
Veja o arquivo de ajuda da função barplot() para ver mais exemplos e outras funcionalidades.
Um histograma é utilizado para representar a distribuição de uma variável aleatória contínua. Basicamente, as freqüências observadas são representadas por classes de ocorrência. As freqüências absolutas podem ser substituídas por freqüências relativas ou proporcionais.
Um dos principais aspectos na construção de um histograma é a definição do número de classes. Existem várias proposições sobre esse aspecto. No R algumas dessas proposições estão implementadas. Inicialmente, vamos estudar os comandos básicos do histograma e a seguir, aplicar os diferentes métodos para definição do número de classes.
No R, a função hist() constrói o histograma. Para ver os argumentos dessa função, utilize ?hist ou args(hist) para ver quais argumentos são possíveis para a função hist().
Como exemplo, considere o seguinte conjunto de dados:
Um simples histograma pode ser gerado da seguinte maneira:
O número de classes pode ser alterado com o comando breaks. Nesse caso são aceitos um simples número indicando quantas classes devem ser formadas. Internamente, há uma função de tolerância que pode não responder ao valor informado. Dependendo da configuração dos dados,o R, automaticamente, faz um ajuste diferente do solicitado.
Veja alguns exemplos
As classes podem ser explicitamente definidas pelo usuário de várias maneiras:
As classes também podem ter tamanhos diferentes:
O argumento right=TRUE, indica que o intervalo de classe é definido da forma (a,b], ou seja, aberto à esquerda e fechado à direita.
O argumento include.lowest=TRUE indica como o R trata das observações que estão nos extremos dos dados. Esse argumento é dependente da opção breaks e rigth.
O número de classes é importante na construção do histograma, pois isso afeta a forma do gráfico e por sua vez, a maneira como os dados ou informações serão interpretadas.
Na função hist()o método de Sturges é o padrão. Esse método define o número de classes, k, através da seguinte expressão k = 1 + log 2(n). Outra opção é utilizar o método ou regra de Scott, onde o número de classes é dado por: k = (2n)1∕3 .
O argumento freq=FALSE define que ao invés de serem inseridas as freqüências no histograma deve-se inserir as proporções ou probabilidades. Dessa maneira, o R insere as barras do histograma de modo que elas tenha uma área de valor 1.
Observe nesse gráfico, que no eixo y aparecem as probabilidades e não as freqüências.
Quando a função hist() é utilizada, algumas informações são geradas. Por exemplo:
Essas informações podem ser utilizadas, por exemplo, na identificação ou na inserção de freqüências sobre as barras (figura 2.15).
Em um histograma, pode-se ter interesse em visualisar a densidade de dados por cada classe. A função rug() insere no gráfico pequenas linhas, indicando a posição dos pontos em daca barra do histograma. Pode acontecer que dados iguais ocorram em um classe. Nesse caso, pode-se utilizar a função jitter() que adiciona uma certa quantidade a cada observação, permitindo que dados iguais possam ser diferenciados.
Em alguns casos, principalmente se existirem muitos dados, essas funções podem não ser muito úteis.
Experimente, também, trabalhar com cores, linhas (density), legendas etc.
Dentro do pacote MASS há uma função que faz histogramas e também dentro do pacote lattice. Veja quais são os argumentos de cada função, compare com a função hist e tente construir alguns gráficos.
Gráficos que mostram a dispersão de dados são úteis para identificar muitas características de dados. Além da dispersão, outliers, tendências entre outros aspectos, podem ser explorados com gráficos de dispersão ou Scatter plots.
No R, além da função plot(), outras funções como stripchart() e dotchart() podem ser utilizados para representar pontos.
Dependendo do tipo de objeto que está sendo utilizado, um simples vetor ou uma matriz, cada função gerará gráficos de acordo com a antureza dos dados.
A função stripchart() produz um gráfico unidimensional, ou seja, considerando apenas
uma escala. Um gráfico de pontos  pode ser uma alternativa a um boxplot,
principalmente quando o número de pontos é pequeno.
pode ser uma alternativa a um boxplot,
principalmente quando o número de pontos é pequeno.
Inicialmente, explore os argumentos da função stripchart():
Como exemplo, vamos considerar o seguinte conjunto de dados:
Outras opções podem ser inseridas. Em especial, o método de posicionamento dos pontos é relevante, pois, por exemplo, observações com o mesmo valor podem passar despercebidas em um gráfico desse tipo. Assim, existem três opções nesse aspecto: overplot, que insere os pontos sobrepostos, jitter, insere os pontos com um "ruído"e stack, que insere os pontos um sobre o outro, como se fosse uma pilha de tijolos.
Quando os dados estão agrupados por grupos ou categorias, a função stripchart() constrói um gráfico, separando as categorias, da seguinte maneira
Experimente, por exemplo, inserir as médias no gráfico:
A função dotchart() é utilizada visualizar os dados, na ordem em que são fornecidos. Antes de iniciar, veja quais são os argumentos dessa função.
Como exemplo, considere o seguinte conjunto de dados:
Um gráfico pode ser construído da seguinte maneira:
Também, se os dados estiverem em uma ordem, o mesmo conjunto de dados é visualizado de outra maneira:
Se os dados estiverem na forma de grupos
Para finalizar, procure alterar os argumentos fornecidos para as funções dotchart() e stripchart(). Experimente também, estudar outros argumentos e trabalhar com outros dados.
Existem muitos gráficos para análsie exploratória de dados. Nesta seção, veremos alguns outros gráficos que podem ser utilizados para resumir informações. No R, alguns desses gráficos são inseridos em pacotes (packages).
Por exemplo, no pacote gplots existem algums funções gráficas para explorar dados.
A função baloonplot() resume as informações em uma tabela mas, há algumas características que podem ser acrescentadas nessa tabela.
Primeiro, é necessárioa carregar o pacote gplots.
Veja o exemplo:
|
> set.seed(12) > vendas.mar <- sample(100:1000, 50) > vendas.abr <- sample(100:800, 50) > marca <- rep(LETTERS[1:5], each = 10) > cidade <- c("Curitiba", "Maringá", "Londrina", "Cascavel", + "Foz do Iguaçu") > cidades <- rep(cidade, 10) > dados <- data.frame(cidades, marca, vendas.mar, vendas.abr) > balloonplot(dados$marca, dados$cidades, dados$vendas.mar)
|
Experimente verificar quais são os argumentos da função e tente modificar alguns argumentos do exemplo acima.
Outro gráfico exploratório, pode ser construído com a função pairs(). Essa função relaciona as variáveis contidas em um ’data frame’ ou matriz, formando uma matriz de dispersão de dados. Veja o resultado da função aplica aos dados de vendas:
Dentro do pacote Hmisc, experimente utilizar a função bpplot(). Essa função cria um boxplot, considerando os percentis de cada variável. Essaa função retorna um gráfico para a varíavel parecido com o boxplt mas, as observações da variável são orepresentadas pela largura do boxplot.
A função ecdf, dentro do pacote Hmisc, constrói um gráfico com a função de distribuição empírica acumulada dos dados. É um gráfico onde a ordem de cada observação é inserida no gráfico em função de cada observação na amostra.
Em muitas análises estatísticas, um dos pressupostos mais comuns é de que a variável aleatória em estudo tenha distribuição Normal. Além de vários testes de hipóteses existentes para realizar essa avaliação, existem, também, maneiras gráficas de se avaliar se uma variável aleatória possui ou não distribuição Normal.
Um desses métodos gráficos, bastante utilizado, é o Gráfico Normal de Probabilidade. No R, a função qqnorm() constrói o gráfico.
Esse gráfico também pode ser utilizado para avaliar se existem outliers ou efeitos significativos de fatores em experimentos planejados.
Considere a figura 2.26, representando uma Distribuição Normal.
A probabilidade percentual P de ocorrência de algum valor menor do que x é dada pela área a esquerda de x.
Fazendo um gráfico para todos os possíveis valores de P vs x obtém-se a curva normal acumulada, que tem a característica sigmóide (forma de S, figura 2.27).
Para gerar o gráfico normal de probabilidade, faz-se um ajuste na escala vertical (P) de modo a se obter uma linha reta. Considere uma amostra de 10 pontos (n=10). A primeira observação (ordenada) apresenta os primeiros 10% da distribuição acumulada da variável. A segunda representa 20% e assim por diante. Considerando que a para estabelecer uma reta a partir da curva acumulada o ponto central (50% ou 0.5) permanece o mesmo, o ajuste pode ser realizado em relação ao centro ou 0.5. Ou ainda, a cada 10% pode-se considerar o ponto intermediário da classe para refazer o gráfico de P vs x. Assim, de forma geral tem-se
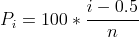
onde i = 1, 2, 3,…,n representa a posição da observação na amostra ordenada e n o tamanho da amostra ou no caso de um experimento, o número de efeitos.
Um gráfico das observações ordenadas vs os valores percentuais Pi indica o comportamento da variável.
No caso da avaliação da Normalidade de uma variável, espera-se que a maioria dos pontos esteja sobre a reta e concentrados na região central. Nas caudas, como se espera para uma distribuição Normal, podem aparecer pontos não muito concentrados e um pouco afastados da reta. Pontos muito distantes e afastados da reta indicam um possível outlier ou dado discrepante.
Em se tratando de um experimento, nesse gráfico, tem-se que tentar avaliar quais são os efeitos que não devem estar ocorrendo ao acaso. Isso pode ser identificado de forma subjetiva pelos pontos que se afastam de uma linha reta.
Essa linha reta é colocada subjetivamente sobre os pontos. Uma sugestão (Montgomery, 2001) é estabelecer uma reta entre os pontos nos quantis 25% e 75%.
Para saber quais são os efeitos significativos basta observar quais são os pontos no gráfico que se afastam da reta e identificar os efeitos correspondentes.
Exemplo de dados de um experimento:
Para construir o gráfico, inicialmente necessitamos das estimativas dos efeitos dos fatores do experimento. Considere o exemplo de um experimento fatorial 24 com uma repetição. Os efeitos estimados são apresentados na tabela 2.1:
|
As probabilidades de cada um dos efeitos são obtidas por P = 100 * (i - 0, 5)∕15. Assim, os resultados para construção do gráfico são apresentados na tabela 2.4.5
|
|
As probabilidades de cada um dos efeitos são obtidas por P = 100 * (i - 0, 5)∕15.
O gráfico é obtido quando os efeitos vs P são colocados em um gráfico de dispersão. Uma linha reta entre os valores dos efeitos ajuda a verificar quais são os pontos que podem ser considerados como significativos.
Essa linha reta é colocada subjetivamente sobre os pontos. Uma regra (Montgomery, 2001) é ligar os pontos nos quantis 25% e 75%.
Os efeitos são:
Ordenando
Aplicando os percentuais acumulados para os efeitos tem-se os seguintes valores:
Esses valores podem ser obtidos através da seguinte função no R:
O gráfico (figura 2.28) é obtido pelo comando plot():
Para fazer a linha, podemos encontrar os quantis dos efeitos,
Utilizando o comando locator() pode-se fazer uma linha entre os pontos dos quantis 25% e 75%. Depois do comando, clique nos pontos correspondentes no gráfico e uma linha será criada.
Você pode usar, também, o comando locator:
Os efeitos significativos podem ser identificados com o comando identify(). Lembre-se que os efeitos estão ordenados do menor para o maior.
Para terminar, aperte o botão direito do mouse (Linux). No Windows, aperte o botão direito e selecione stop.
Faça agora o Gráfico Normal de Probabilidade gerado pelo R. Compare os gráficos.
Experimente a opção
E agora?
Em algumas situações, pode ser de interesse fazer gráficos de funções relacionadas à algumas distribuições. Nesta seção, veremos como utilizar a função curve() para gerar alguns gráficos dessa natureza.
Por exemplo, vamos utilizar inicialmente a distribuição Normal.
A distribuição Weibull, pode ser representada da seguinte forma:
E a distribuição Gama, da seguinte maneira:
Em cada uma destas distribuições, modifique os parâmetros para entender o comportamento de cada uma.
Sugestão de exercícios
Experimente construir o gráfico de outras distribuições. Como sugestão, experimente a distribuição F, χ2 e t.
A função coplot() pode ser utilizada para representar dados que podem ser arranjados da forma respã∥b, onde a e b são variáveis do tipo fator. Em geral, modelos estatísticos podem ser escritos sob essa forma. Uma plicação está na análise de dados experimentais, por exemplo.
Como exemplo, considere o seguinte conjunto de dados
A função coplot() pode ser utilizada da seguinte maneira:
Interprete o gráfico!
Experimente, também, inverter os fatores:
Em algumas análises, gráficos tridimensionais podem ser gerados para visualização do comportamento de modelos estatísticos.
Entre os mais comuns está o gráfico de superfície de resposta. Este tipo de gráfico é gerado a partir de modelos que expressam o comportamento de uma variável resposta em função de dois ou mais fatores.
Não abordaremos aqui o ajuste de modelos. Faremos apenas o uso de modelos pré-existentes
Para construir o gráfico de superfície de resposta são necessárias três variáveis, ou seja, x e y, representando os níveis dos fatores e uma variável z, representando o comportamento da variável resposta.
Como exemplo, considere uma variação de x e y da seguinte forma
Os valores preditos pelo modelo, nessa escala de variação, podem ser preditos por uma função ou um modelo
Alternativamente, os coeficientes do modelo podem ser obtidos diretamente do modelo (nesse caso ele não existe, apenas apresentamos a forma)
Antes de construirmos o gráfico, veja como as três variáveis x, y e z estão organizadas.
Para gerar o gráfico, os dados precisam ser agrupados de forma a serem utilizados pela função persp.
A função outer prepara os dados para serem utilizados pela função persp.
Para mais detalhes dessa função utilize
Para construir a superfície, utilize a função persp da seguinte maneira:
Experimente alterar alguns argumentos e entender sua funcionalidade.
Os mesmos dados podem ser representados de duas outras formas. Através de curvas de nível com a função countour() ou de um gráfico representando a variável z por cores com a função image().
Uma curva de nível pode ser construída com a função countour(). Observe que cada curva corresponde a uma ’altura’ da variável resposta
Investigue a função curve() e experimente alterar algumas opções.
Uma outra alternativa aos gráficos anteriores é construir um gráfico de cores para representar o modelo. A função image() pode ser utilizada nesse caso.
VEja o seguinte exemplo:
Para finalizar, considere que o ponto máximo (nesse caso) corresponde a 168 minutos e 151,5 graus. A representação pode ser feita da seguinte forma
Para finalizar, experimente utilizar alguns exemplos do pacote lattice:
Experimente também a utilizar a função scatterplo3d() do pacote do mesmo nome: