Sensoriamento Remoto II, Prof. Dr.Ing. Jorge Centeno - UFPR

Transformação das Componentes Principais

Revisão de matemática: A figura ao lado mostra um recorte da banda do verde de uma imagem Landsat, onde foram selecionadas duas regiões (A em vermelho e B em amarelo). Comparando as tonalidades destas regiões, o que poderia concluir? Bem provavelmente diríamos que a região B é mais escura que a região A. Esta afirmação pode ser corroborada comparando a média dos valores digitais das duas regiões. Na tabela são mostradas as médias e é evidente que a média de B é menor que a de A. Traduzindo isto a níveis de cinza diríamos que B é mais escura que A.

Uma segunda observação seria possível a respeito da variação dos valores em cada região. Mas, como medir a uniformidade? O conceito de uniformidade nos remete ao conceito de dispersão dos valores. Se os valores forem muito parecidos entre si, então diriamos que a região é uniforme. Se os valores são muito dispersos, então a reg´ão é menos uniforme. O conceito de dispersão está presente no desvio padrão. O desvio padra (d.p.) mede a dispersão dos valores em torno da média. A média é calculada como:

A diferença entre um valor qualquer e a média nos daria o afastamento do valor em relação a esta referência.

Porém, se existem diferenças positivas, valores acima da média, e negativas, valores abaixo da média, esta medida pode ser zerada mesmo em situações onde a dispersão é alta, dando assim informação errada. Então, para contornar este problema adota-se o quadrado da diferença. Isto equivale a calcular a distância média em valor absoluto. Bem, como a função quadrado é monotônica crescente, usar a distância ou o quadrado da distância não vai mudar a situação para fins de comparação, então, podemos usar o quadrado, do que se deriva a medida da variância.

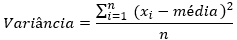
O desvio padrão não é mais do que a raiz da variância. Descreve o mesmo, mas a diferença é que ele está nas mesmas unidades que a variável.

Analisando as estatísticas dos dois recortes (A e B), é constatado que o desvio padrão de A é maior que o de B, logo pode-se dizer, mesmo sem olhar à imagem, que A tem maior variação de valores, dispersão, do que B, que é mais uniforme.

Para terminar, abra a imagem Landsat da Ilha do Mel/PR ( mel600.lan) e selecione uma área contendo várias classes de cobertura, pode ser grande. Para isto, use a opção de seleção de amostras de treinamento que usamos nas aulas de sensoriamento remoto 1.

No Multispec

  • processor + statistics + OK. Isto habilita a janela de projeto.
  • Confirme a ação na janela seguinte. Não se preocupe em dar nome à classe.
  • Agora, na janela de projeto selecione Classes. Isto mostrará que você tem uma classe "Class 1", apenas.
  • Na mesma janela, clique no campo onde consta List Classes Stats para listar as estatísticas desta classe. Para isto, escolha List Stats..., a última opção.
  • Na nova janela, que aparece após list Stats..., verifique se a opção Mean & standard deviation (Média e desvio padrão) está selecionada. A seguir, confirme com OK. O programa perguntará se pode atualizar o projeto. Claro que sim! Se não, como poderíamos calcular as estatísticas?
  • Agora você pode encontrar as estatísticas da imagem na janela de texto text Output.

    Pergunta: Qual banda é a mais clara? e a mais escura? Qual banda é mais uniforme? e a menos uniforme?

    Após minutos de pensar, deseja conferir se acertou? Clique aqui para conferir.

    Para continuar voce pode voltar ao menu principal ou continuar para a próxima aula .

    Copyright © 2020
    Jorge Centeno: centeno@ufpr.br