CENTENO

Transformação das Componentes Principais

imagem RGB

componentes principais

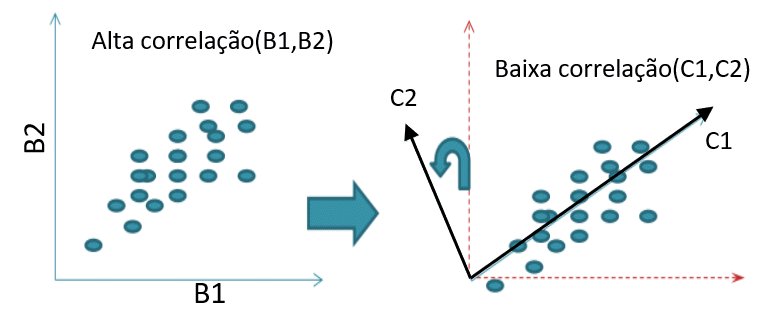
Veja a figura ao lado. Na primeira figura mostra-se um conjunto de pontos altamente correlacionados no sistema (B1, B2). Eles poderiam ser, por exemplo, as leituras do valor digital em duas bandas de uma imagem de satélite. Por serem altamente correlacionadas, estas bandas serão muito parecidas e o conjunto altamente redundante. Podemos dizer, com baixa margem de erro, que a informação contida em uma imagem pode ser usada para calcular a segunda. Então, para que armazenar duas imagens? Não bastaria uma? Porém, mesmo havendo correlação entre B1 e B2, ao escolhermos apenas uma delas perderíamos parta de informação, pois as imagens não são idênticas.
E se efetuássemos uma rotação, como mostrado na segunda figura, o eixo C1, ao passar pela direção de maior espalhamento dos pontos, não resumiria o conteúdo das duas imagens? Este novo sistema (C1,C2) é ainda ortogonal, é uma rotação do sistema (B1,B2), mas tem a característica de que nele os dados não são correlacionados. Em se tratando de duas variáveis, a rotação é simples, mas quando se lida com, por exemplo, 5 bandas? como obter a rotação?

Transformação das componentes principais:
Do ponto de vista estatístico, o objetivo da transformação das componentes principais consiste em representar um conjunto de dados usando um novo conjunto de variáveis, combinações lineares das originais. Este novo sistema deve ter como propriedade um baixo grau de correlação entre as novas variáveis.
A transformação das componentes principais consiste basicamente numa rotação dos dados no espaço das bandas e os coeficientes da rotação podem ser obtidos com ajuda dos autovetores. Ou seja, as componentes do novo sistema resultam da projeção do sistema original na direção dos autovetores da matriz de covariância. Considerando 3 bandas: C = M * B Considerando as 3 bandas do visível da imagem da Ilha do Mel (ao lado), isto equivale a: |C1| | v11 v12 v13 | |B1|
|C2|= | v21 v22 v23 |*|B2|
|C3| | v31 v32 v33 | |B3|
Veja, a seguir, a matriz de correlação da imagem RGB e da imagem das componentes principais. valeu a pena? Channel 1      2      3        Channel 1       2       3
        1 1.00                         1 1.00
        2 0.91 1.00                    2 0.00 1.00
        3 0.83 0.95 1.00               3 0.00 -0.00 1.00
Agora veja o resultado, na figura ao lado. Percebe que a primeira componente parece uma imagem preto e branco? Ela tem muita informação das três bandas originais. Já a terceira parece ruidosa, pois o conteúdo de informação desta nova componente é baixo. O teor de informação de cada componente é proporcional ao tamanho relativo do autovetor associado. Inf(i) = Li/(L1+L2+L3)

Para continuar voce pode voltar ao menu principal ou continuar para o próximo módulo de prática Componentes Principais .