 //
//
Nesta última fase você deve implementar o algoritmo DiVHA de forma a mostrar quais os testes são executados para diferentes configurações de falha. Não é necessário simular um sistema executando o DiVHA, apenas listar os testes necessários.
O programa deve permitir dois modos de uso diferentes:
No primeiro o usuário entre com o número de nodos do sistema e a lista de nodos falhos, a partir do que é fornecida como saída a lista de testes para aquele sistema específico. Neste modo de uso o usuário pode ainda entrar apenas com o número de nodos do sistema e o número de nodos falhos, que são escolhidos aleatoriamente pelo programa.
O segundo modo de uso envolve uma execução exaustiva, para sistemas com n=2, 4, 8, ... até infinitos nodos. Para cada valor de n, testar todas as combinações de falhas, dizendo o número de testes executados.
Atenção: são duas semanas de prazo, organize-se para completar de maneira adequada. Cada dia de atraso serão descontados 25% da nota.
Deve ser feita uma página Web, que contém:
Relatório HTML explicando como o trabalho foi feito (use desenhos, palavras, o que você quiser): o objetivo é detalhar as suas decisões para implementar seu trabalho. Código fonte dos programas em C, comentados.
ATENÇÃO: acrescente a todo programa a terminação ".txt" para que possa ser diretamente aberto em um browser. Exemplos: cliente.py.txt ou servidor.c.txt
Log dos testes executados: mostre explicitamente diversos casos testados, lembre-se é a partir desta listagem de testes que o professor vai medir até que ponto o trabalho está funcionando.
Implementação do DiVHA (Distributed Virtual Hypercube Algorithm):
DiVHA considera um sintema com N nodos em estado de falha ou sem-falha totalmente conectado e com as conexões livres de falha. O diagnóstico distribuído busca diminuir o tempo de latência da diagnose. No pior caso uma rodada do DiVHA pode executar (n*n)/4 testes. A latência é de no máximo log2 N rodadas de testes, e na maioria dos testes executa N*log2*N testes por rodada. Os nodos sem falha executam seus testes e reportam os resultados. O grafo testing graph é chamado T(S). Quando o nodo i testa um nodo sem falha j, recebe informação de todos k nodos com distância menor ou igual a log2*n-1 no hipercubo. A distância no hipercubo entre os nodos i e j, chamada h(i,j), o número de arestas no menor caminho entre o nodo i e j. O DiVHA emprega esta estrégia para adicionar arestas preservando a propriedade logaritmica do hipercubo e sua topoligia no caso de nodos falhos
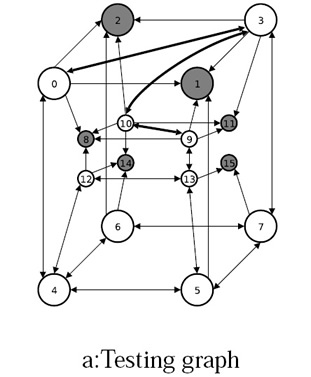
*Grafo de teste:*
A imagem abaixo mostra o hypercube virtual de exemplo, considerando o nodo 4
falho e os outros nodos sem-falha. As arestas pontilhadas representam
as arestas extras que existiam antes do nó 4 se tornar falho.//
 //
//
Iterações com os clusters: 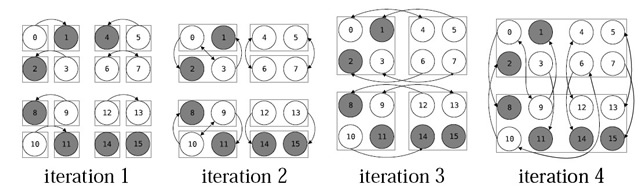 //
//
Esta função devolve quais os nodos que o nodo i deve testar no cluster s.
Contém toda a estrutura e métodos do grafo de testes. O grafo de testes foi implementado usando uma matriz dinâmica de adjacências e foi usado o algoritmo Dijkstra para calcular os caminhos mais curtos entre nodos, este algoritmo apresenta complexidade O(n2) para seu pior caso.
Exemplo de grafo: 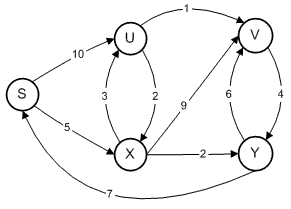 //
//
Sua respectiva matriz de adjacências: 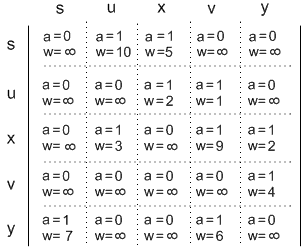 //
//
Implementação
O programa criado deve ser executado seguindo o seguinte formato:
./trab3 nºdimensões nodo_falho[1] nodo_falho[2] ... nodo_falho[n]
Sendo que os nodos falhos são facultativos.
LOGS:
log1: Hipercubo de 2 dimensões, sem nodos falhos. Executado em 0m0.002s.
log2: Hipercubo com 3 dimensões, sem nodos falhos. Executado em 0m0.002s.
log2: Hipercubo com 3 dimensões e os nodos 2 e 5 falhos. Executado em 0m0.003s.
log4: Hipercubo com 4 dimensões, tentado falhar nodo 22, fora do interval válido (16).
log5: Hipercubo de 6 dimensões com os nodos 3 7 12 22 30 35 40 43 51 60 falhos. Executa em 0m0.316s.
log6: Hipercubo de 7 dimensões com os nodos 7 3 18 23 falhos. Executado em 0m6.440s. falhos. Executados em .
log7 Hipercubo de dimensão 8 se nodos falhos. Executado em 1m57.429s.
log7a Hipercubo de dimensão 8 com os nodos 3 13 23 33 43 falhos. Executado em 1m55.863s.
log8 Hipercubo de 8 dimensões com os nodos falhos: 4 9 13 26 32 47 56 66 78 82 93 101 123 144 167 182 199 200 201 214 222 230 244 252. Executado em 1m46.951s.
log9: Hipercubo de 9 dimensões sem nodos falhos. Executados em 34m58.864s.
log10 Hipercubo de 9 dimensões com os nodos 3 7 12 22 30 35 40 43 51 60 66 77 83 88 91 99 falhos. Executado em 33m56.423s
log11: Hipercubo de 10 dimensões sem nodos falhos executado em 632m31.007s.
Com 12 dimensões o processamento não terminou em mais de 30 horas de execução com processador a 100% e apresentando crescimento na memória utilizada. Este foi o limite com tempo aceitável de espera desta atividade.
O número de testes nunca é superior a N*Log N (máximo).
Observando os tempos, podemos concluir com base nos testes que os testes com nodos falhos foram mais rápidos. Também podemos observar a enorme diferença de tempo entre as execuções, o crescimento é exponencial. Podemos observar no hipercubo de 8 dimensões um tempo de aproximadamente 2 minutos, já no hipercubo de 9 dimensões em torno de 30 minutos e no de 10 dimensões mais de 10 horas.
Apenas para ilustrar, seguem imagens de um hipercubo de 6 e um de 9 dimensões, demostrando o quão complexas são estas estruturas:
Hipercubo 6: 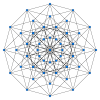 //
//
Hipercubo 9:  //
//
Referências:
Self Diagnosis Based on the DistributedVirtual Hypercube Algorithm
Luis C. E. Bona1 , Elias P. Duarte Jr2 , Keiko V. O. Fonseca1 artigo