![]()
Essência da teoria da relatividade.
O desenvolvimento da eletrodinâmica levou à revisão das noções de espaço e tempo.
De acordo com as noções clássicas de espaço e tempo, consideradas inabaláveis ao longo dos séculos, o movimento não exerce nenhuma influência no tempo (o tempo é absoluto), e as medidas lineares de qualquer corpo não dependem do fato de o corpo estar em movimento ou não (o comprimento é absoluto) .
A teoria da relatividade especial de Einstein é um novo estudo do espaço e do tempo, vindo substituir as noções antigas (clássicas).
O princípio da relatividade na mecânica e na eletrodinâmica.
Depois de Maxwell, na segunda metade do séc. XIX, ter formulado as leis fundamentais da eletrodinâmica, surgiu a seguinte questão: será que o princípio da relatividade, verdadeiro para os fenômenos mecânicos, se estende aos fenômenos electromagnéticos? Por outras palavras, decorrerão os processos electromagnéticos (interação da cargas e correntes, propagação das ondas eletromagnéticas, etc.) igualmente em todos os sistemas inerciais? Ou ainda, o movimento uniforme e retilíneo, não influenciando os fenômenos mecânicos, exercerá alguma influência nos processos eletromagnéticos?
Para responder a esta questão era necessário verificar se se modificariam as leis principais da eletrodinâmica na passagem de um sistema inercial para outro ou se, à semelhança das leis de Newton, elas se conservariam. Só no último caso seria possível deixar de duvidar sobre a veracidade do princípio da relatividade nos processos electromagnéticos e considerar este princípio como uma lei geral da Natureza.
As leis da eletrodinâmica são complexas e a resolução deste problema não era nada fácil. No entanto, raciocínios simples pareciam ajudar a encontrar a resposta certa. De acordo com as leis da eletrodinâmica, a velocidade de propagação das ondas electromagnéticas no vácuo é igual em todas a direções e o seu valor é c = 3.1010 cm/s. Mas, por outro lado, de acordo com o princípio da composição de velocidades da mecânica de Newton, a velocidade só pode ser igual a c num dado sistema. Em qualquer outro sistema, que se mova em relação ao sistema dado com velocidade v , a velocidade da luz deveria ser igual a
![]()
Isto significa que se é verdadeiro o princípio da composição de velocidades, então, na passagem de um sistema inercial para outro, as leis da eletrodinâmica deverão alterar-se de tal modo que neste sistema a velocidade da luz, em vez de ser igual a c ,será igual a
![]() .
.
De forma verificou-se que existiam algumas contradições entre a eletrodinâmica e a mecânica de Newton, cujas leis estão de acordo com o princípio da relatividade. As tentativas de resolver as dificuldades que surgiram foram feitas em três direções diferentes.
A primeira possibilidade consistia em declarar que o princípio da relatividade não se podia aplicar aos fenômenos electromagnéticos. Este ponto de vista foi defendido pelo grande físico holandês G. LORENTZ, fundador da teoria eletrônica. Os fenômenos electromagnéticos eram vistos, desde o tempo de Faraday, como processos que decorriam num meio especial, que penetra em todos os corpos e ocupa todo o espaço - " o éter mundial " . Um sistema inercial parado em relação ao éter é, segundo Lorentz, um sistema privilegiado. Nele, as leis da eletrodinâmica de Maxwell são verdadeiras e têm uma forma mais simples. Só neste sistema a velocidade da luz no vácuo é igual em todas as direções.
A segunda possibilidade consiste em considerar as equações de Maxwell falsas e tentar modificá-las de tal modo que com a passagem de um sistema inercial para outro (de acordo com os habituais conceitos clássicos de espaço e de tempo) não se alterem . Tal tentativa foi feita, em particular, por G.HERTZ. Segundo Hertz, o éter é arrastado totalmente pelos corpos em movimento e por isso os fenômenos electromagnéticos decorrem igualmente, independentemente do fato do corpo estar parado ou em movimento. O princípio da relatividade é verdadeiro.
Finalmente, a terceira possibilidade da resolução das dificuldades consiste na rejeição das noções clássicas sobre o espaço e tempo para que se mantenha o princípio da relatividade e as leis de Maxwell. Este é o caminho mais revolucionário, visto que significa a revisão das mais profundas e importantes noções da física. De acordo com este ponto de vista, não são as equações do campo magnético que estão incorretas, mas sim as leis da mecânica de Newton, as quais estão de acordo com a antiga noção de espaço e tempo. É necessário alterar as leis da mecânica, e não as leis de eletrodinâmica de Maxwell.
Só a terceira possibilidade é que é correta. Einstein desenvolveu-a gradualmente e criou uma nova concepção do espaço e do tempo. As duas primeiras possibilidades vieram a ser rejeitadas pela experiência.
Quando Hertz tentou mudar as leis da eletrodinâmica de Maxwell verificou-se que as novas equações não podiam explicar muitos fatos observados. Assim, de acordo com a teoria de Hertz, a água em movimento deverá arrastar completamente consigo a luz que se propaga nela, visto que ela arrasta o éter, onde a luz se propaga. A experiência mostrou que na realidade isso não se passava.
A experiência de Michelson. O ponto de vista de Lorentz, de acordo com o qual deve existir um certo sistema de referência, vinculado ao éter mundial, que se mantém em repouso absoluto, também foi rejeitado por experiências diretas.
Se a velocidade da luz só fosse igual a 300 000 km/s num sistema vinculado ao éter, então, medindo a velocidade da luz em qualquer outro sistema inercial, poder-se-ia observar o movimento deste sistema em relação ao éter e determinar a velocidade deste movimento. Tal como num sistema que se mova em relação ao ar surge vento, quando se dá o movimento em relação ao éter (isto, claro, admitindo que o éter existe) deveria surgir "vento de éter". A experiência para verificação do "vento de éter" foi realizada em 1881 pelos cientistas americanos A. MICHELSON e E. MORLEY, segundo uma idéia avançada 12 anos antes por Maxwell.
Nesta experiência compara-se a velocidade da luz na direção do movimento da Terra e numa direção perpendicular. A medição foi feita com grande exatidão com o auxílio de um instrumento especial - interferômetro de Michelson. As experiências foram realizadas a diferentes horas do dia e em diferentes épocas do ano. Mas obteve-se sempre um resultado negativo: não foi possível observar o movimento da Terra em relação ao éter.
Esta situação é semelhante à que se verificaria se, deitando a cabeça de fora pela janela de um automóvel à velocidade de 100 km/h, não sentíssemos o vento soprando contra nós.
Deste modo, a hipótese da existência de um sistema de referência privilegiado também foi rejeitada experimentalmente. Por sua vez, isto significava que não existe nenhum meio especial, "éter", ao qual se possa vincular esse tal sistema privilegiado.
2 - Postulados da Teoria da Relatividade
(Um postulado na teoria física tem o mesmo papel que um axioma na matemática. É uma afirmação fundamental que não pode ser demonstrada logicamente. Na Física o postulado é o resultado da generalização de fatos experimentais.)
Para explicar os resultados negativos da experiência de Michelson e de outras experiências, que deveriam observar o movimento da Terra em relação ao éter, colocaram-se várias hipóteses. Por meio destas hipóteses tentou-se explicar o motivo pelo qual não é possível encontrar um sistema de referência privilegiado (considerava-se que tal sistema existia na realidade). Assim, em particular, para se explicar a experiência de Michelson, formulou-se a hipótese da diminuição dos comprimentos lineares de todos os corpos quando se movem em relação ao éter.
Einstein abordou este problema sob outro ponto de vista: não se devem criar diferentes hipóteses para explicar os resultados negativos de todas as tentativas de verificar a diferença entre sistemas inerciais. As leis da Natureza determinam a igualdade total dos sistemas inerciais de referências em relação não só à mecânica mas também aos processos electromagnéticos. Não há qualquer diferença entre a situação de repouso e o movimento uniforme e retilíneo.
O princípio da relatividade é o postulado principal da teoria de Einstein. Ele formula-se do seguinte modo: todos os processos da Natureza decorrem igualmente em todos os sistemas inerciais de referência.
Isto significa que em todos os sistemas inerciais as leis físicas têm a mesma forma. Deste modo, o princípio da relatividade da mecânica clássica generaliza-se para todos os processos da Natureza, inclusivamente para os electromagnéticos.
Mas a teoria da relatividade não se baseia só no princípio da relatividade. Existe ainda um segundo postulado: a velocidade da luz no vácuo é igual para todos os sistemas de referência inerciais. Ela não depende nem da velocidade do emissor, nem da velocidade do receptor do sinal luminoso.
A velocidade da luz desempenha, deste modo, um papel especial. Além disso, como resulta dos postulados da teoria da relatividade, a velocidade da luz no vácuo é a velocidade máxima possível de transmissão de interação na Natureza.
A formulação dos postulados da teoria da relatividade constituiu uma atitude muito ousada, visto que estes postulados se encontram em contradição com as concepções clássicas do espaço e do tempo.
De fato, admitamos que no instante em que coincidem as origens das coordenadas dos sistemas de referência inerciais K e K1 ( fig. 1), que se movem em relação um ao outro com a velocidade , na coordenada inicial é emitido um sinal luminoso de curta duração. Durante um certo intervalo de tempo t os sistemas afastam-se um do outro até à distância vt, enquanto que a superfície ondulatória esférica terá um raio igual a ct. Os sistemas k e k1 são iguais, e a velocidade da luz é igual em ambos os sistemas.
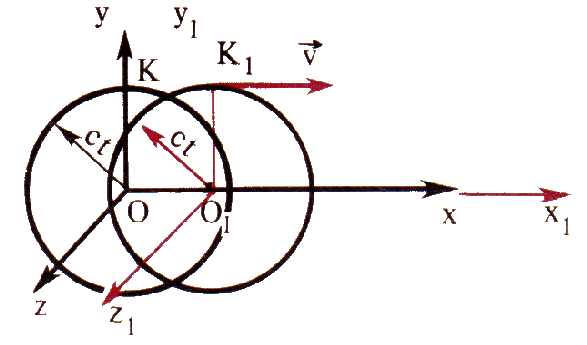
Fig. 1
Consequentemente. do ponto de vista do observador ligado ao sistema de referência K, o centro da esfera encontrar-se-á no ponto 0, enquanto que do ponto de vista do observador, ligado ao sistema de referência K1 , o centro encontrar-se-á no ponto 01 . Mas, como é evidente, uma superfície esférica não pode ter dois centros 0 e 01 . Esta contradição resulta de um raciocínio baseado nos postulados da teoria da relatividade.
Neste caso existe, de fato, uma contradição. Mas não dentro da própria teoria da relatividade. A contradição resulta das concepções clássicas de espaço e de tempo, que, no caso de movimento a grandes velocidades, deixam de ser verdadeiras.
3 - O Caracter Relativo da Simultaneidade
O motivo da inconsistência das noções clássicas do espaço e de tempo é a suposição errada sobre a possibilidade de transmissão instantânea de interação e de sinais de um ponto do espaço para outro. A existência de um limite finito da velocidade de transmissão de interação torna necessária uma mudança profunda da opções habituais de espaço e de tempo, baseadas na experiência quotidiana. O conceito de tempo absoluto , que decorre a um ritmo estabelecido de uma vez para sempre, independentemente da matéria e do tempo, revelou-se incorreto.
Se admitirmos que os sinais se propagam instantaneamente, então a afirmação de que os acontecimentos em dois pontos A e B, separados no espaço, ocorreram simultaneamente terá um significado absoluto. É possível colocar nos pontos A e B relógios e sincronizá-los por meio de sinais instantâneos. Se um sinal desses saiu de A, por exemplo, às 0h 45m e, nesse mesmo instante, chegou ao ponto B, de acordo com o relógio neste ponto, então só dois relógios indicam a mesma hora, ou seja, estão sincronizados. Se não se dá tal coincidência, podem sincronizar-se os relógios, adiantando aquele que indica menos horas no momento da emissão do sinal.
Quaisquer acontecimentos, por exemplo, dois relâmpagos, são simultâneos se ocorrerem quando os relógios sincronizados indiquem a mesma hora.
Só colocando nos pontos A e B relógios sincronizados se pode ajuizar se quaisquer dois acontecimentos nestes pontos se dão ao mesmo tempo ou não. Mas como é que podermos sincronizar relógios que se encontram a uma dada distância um do outro, se a velocidade de propagação dos sinais não é infinitamente grande?
Para sincronizar os relógios é natural recorrer a sinais luminosos ou outros sinais electromagnéticos, visto que a velocidade das ondas electromagnéticas no vácuo é uma grandeza constante, conhecida com exatidão.
É este o método utilizado para verificar as horas pelo rádio. Os sinais de tempo ajudam a sincronizar os nossos relógios com os relógios-padrão exatos. Sabendo a distância entre a estação de rádio e a nossa casa pode-se calcular a correção correspondente ao atraso do sinal. Esta correção, é claro, é muito pequena. Na nossa vida quotidiana ela não tem qualquer significado. Mas no caso das grandes distâncias cósmicas ela pode tornar-se muito importante.
Vejamos detalhadamente um método simples de sincronização de relógios que não exige nenhum cálculo. Suponhamos que um astronauta quer saber se os relógios A e B colocados nos extremos opostos de uma nave espacial ( fig. 2), estão certos entre si. Para isso, com o auxílio de um emissor, parado em relação à nave e colocado no meio dela, o astronauta produziu uma fulguração. A luz atinge ao mesmo tempo ambos os relógios. Se ambos eles marcarem a mesma hora, isso significa que estão sincronizados.
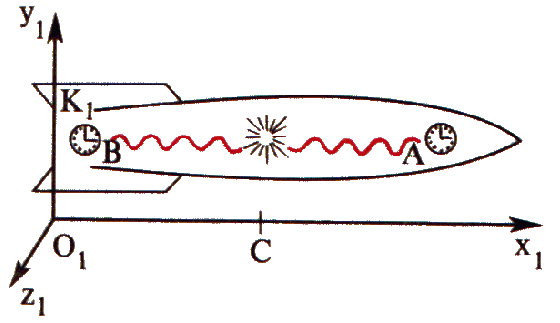
Fig. 2
Mas só será assim em relação ao sistema de referência K1 , ligado à nave. No sistema de referência K, em relação ao qual a nave se move, a situação é diferente . O relógio que se encontra na parte da frente da nave afasta-se do lugar onde se encontra o emissor e, para atingir o relógio A, a luz tem de percorrer uma distância maior do que metade do comprimento da nave (fig. 3 a, b) , pelo contrário, o relógio B aproxima-se do emissor e o caminho percorrido pelo sinal luminoso é menor do que metade do comprimento da nave. Por isso, o observador no sistema K concluiu que os sinais não atingem ambos os relógios simultaneamente.
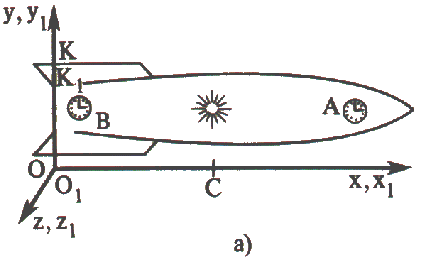
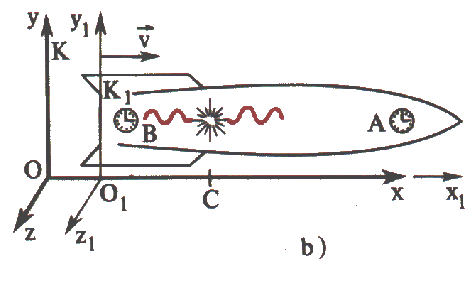
Fig. 3
Dois acontecimentos nos pontos A e B dão-se ao mesmo tempo no sistema K1 e em instantes diferentes no sistema K. Mas de acordo com o princípio da relatividade os sistemas K1 e K são equivalentes. A nenhum destes sistemas se pode dar preferência. Por isso, somos obrigados a concluir que a simultaneidade dos acontecimentos em pontos distintos do espaço é relativa. O motivo do caracter relativo da simultaneidade é, como nós vimos, o valor finito da velocidade de propagação dos sinais.
É devido ao caracter relativo da simultaneidade que se explica o paradoxo dos sinais luminosos esféricos, sobre o qual se falou em 2 . A luz atinge simultaneamente os pontos da superfície esférica com centro no ponto 0, do ponto de vista do observador que se encontra parado em relação ao sistema K. Do ponto de vista do observador, ligado ao sistema K1 , a luz atinge estes pontos em instantes diferentes.
Evidentemente, é verdadeiro o inverso: no sistema K a luz atinge os pontos da superfície esférica com centro em 01 em instantes diferentes, e não ao mesmo tempo, como parece ao observador que se encontra no sistema K1 .
Daqui resulta que na realidade não existe nenhum paradoxo.
4 - As Principais Conseqüências dos Postulados da Teoria da Relatividade
Dos postulados da teoria da relatividade resulta um conjunto de importantes corolários que afetam as propriedades do espaço e do tempo. Nós não nos deteremos na explicação relativamente difícil destes corolários. Limitemo-nos a enumerá-los.
A relatividade da distância
A distância não é uma grandeza absoluta, mas depende do movimento do corpo em relação a um dado sistema de referência.
Designemos por ![]() o comprimento de uma vara no sistema de referência K, em relação ao qual a vara está parada. Então o comprimento
o comprimento de uma vara no sistema de referência K, em relação ao qual a vara está parada. Então o comprimento ![]() , desta vara, no sistema k1 , em relação ao qual a vara se move com velocidade v, determina-se pela fórmula.
, desta vara, no sistema k1 , em relação ao qual a vara se move com velocidade v, determina-se pela fórmula.
![]()
Como se vê por esta fórmula ,
![]() .
.
Nisto consiste a redução relativista do corpo nos sistemas de referência em movimento.
Relatividade dos intervalos de tempo.
Seja o intervalo de tempo entre dois acontecimentos que se dão no mesmo ponto do sistema inercial K igual a t0 . Tais acontecimentos podem ser, por exemplo, dois batimentos de um metrônomo que conta os segundos.
Então o intervalo t entre estes acontecimentos, num sistema de referência k1 , que se move em relação ao sistema K com a velocidade v, exprime-se do seguinte modo.
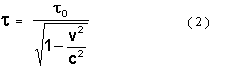
Evidentemente t > t 0 . Trata-se do efeito relativista de atraso do tempo nos sistemas de referência em movimento.
Se tivermos v << c , nas fórmulas ( 1 ) e ( 2 ) pode desprezar-se a grandeza v2/c2. Então será
![]()
ou seja, a redução dos corpos e o atraso do tempo relativistas num sistema de referência em movimento podem não ser tomados em consideração.
A lei relativista da composição das velocidades. Aos novos conceitos relativistas de espaço e de tempo corresponde uma nova lei da composição das velocidades. Evidentemente que a lei clássica da composição das velocidades não pode ser verdadeira, visto que ela contradiz a afirmação de que a velocidade da luz é constante na vácuo.
Se um comboio se move com a velocidade v e num vagão, segundo a direção do movimento do comboio, se propaga uma onda luminosa, então a sua velocidade em relação á Terra deve ser igual de novo a c , e não a v + c . A nova lei da composição das velocidades deve conduzir ao resultado pretendido.
Formularemos a lei da composição das velocidades para o caso particular em que o corpo se movimenta ao longo do eixo X1 do sistema de referência K1 , o qual, por sua vez, se move com a velocidade v em relação ao sistema de referência K. Além disso, os eixos das coordenadas X e X1 coincidem sempre, enquanto os eixos das coordenadas Y e Y1 , Z e Z1 se mantêm paralelos (fig. 4) .
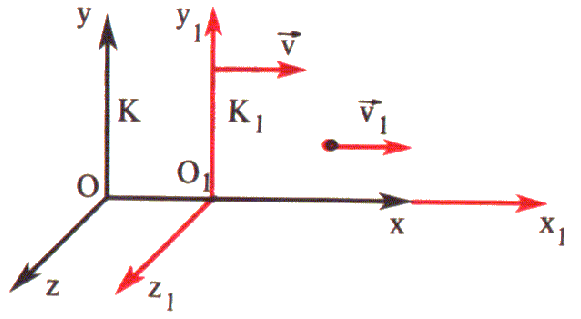
Fig. 4
Representemos a velocidade do corpo em relação a K1 por v1 , a velocidade do mesmo corpo em relação a K por v2 . Então, de acordo com a lei relativista da composição de velocidades,
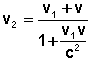
Se v << c e v1 << c , então podemos desprezar o termo v1v / c2 no denominador e, em vez de (3) , obtermos a lei clássica da composição das velocidades:
v2 = v1 + v
Quando v1 = c , a velocidade v2 também se torna igual a c , tal como exige o segundo postulado da teoria da relatividade . De fato,
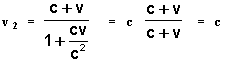
Uma admirável propriedade da lei relativista da composição de velocidades consiste em que, para quaisquer velocidades v1 e v (evidentemente, não superiores a c ) a velocidade v2 não é superior a c . No caso limite em que v1 = v = c obtém-se
![]()
A velocidade v > c não é possível. A esta conclusão também se pode chegar através de raciocínios formais. De fato, se v > c , as fórmulas (1) e (2) perdem o significado, visto que o comprimento e o tempo se tornam imaginários.