Aula 02: Delineamento Completamente Casualizado

Objetivo desta Aula

O objetivo desta aula é utilizar o software R para realizar a análise de variância de um experimento conduzido no Delineamento Completamente Casualizado.

Trabalhando com o arquivo de dados

A seguir são apresentados os comandos para a análise do experimento. Procure entender o que cada comando executa e compare as saídas com os resultados apresentados em sala de aula.

Inicialmente, o arquivo de dados está disponível em arquivo de dados que deve ser copiado para o seu diretório de trabalho.

ex01 <- read.table("exemplo01.txt", head=T)
ex01

Caso o arquivo esteja em outro diretório deve-se colocar o caminho completo deste diretório no argumento de read.table acima.
A seguir vamos inspecionar o objeto que armazena os dados e suas componentes:

is.data.frame(ex01)
names(ex01)

ex01$resp
ex01$trat

is.factor(ex01$trat)
is.numeric(ex01$resp)

Portanto, o objeto é um data.frame com duas variáveis, sendo uma delas um fator (a variável trat) e a outra uma variável numérica.

Nota: na ANOVA, as vaiáveis independentes precisam possuir a característica ''factor´´. Caso contrário, o R realizará uma análise de regressão entre as variáveis.

Análise descritiva

Vamos agora fazer uma rápida análise descritiva:

summary(ex01)
tapply(ex01$resp, ex01$trat, mean)

Há um mecanismo no R de ``anexar'' objetos ao caminho de procura que permite economizar um pouco de digitação. Veja os comandos abaixo e compara com o comando anterior.

search()

attach(ex01)
search()

tapply(resp, trat, mean)

Pode-se ''desanexar´´ o objeto com os dados (embora isto não seja obrigatório) com o comando.

detach(ex01)

Quando um objeto do tipo list ou data.frame é anexado no caminho de procura com o comando attach() faz-se com que os componentes deste objeto se tornem imediatamente disponíveis e portanto pode-se, por exemplo, digitar somente trat ao invés de ex01$trat.

Prosseguindo com a análise exploratória:

ex01.m <- tapply(resp, trat, mean)
ex01.m

ex01.v <-  tapply(resp, trat, var)
ex01.v

plot(ex01)
points(ex01.m, pch="x", col=2, cex=1.5)

ANOVA

O comando aov, realiza a análise dos dados do data.frame
Compare a saída do comando aov com o comando ANOVA.

ex01.av <- aov(resp ~ trat, data = ex01)
ex01.av

summary(ex01.av)
anova(ex01.av)

Portanto o objeto ex01.av guarda os resultados da análise de variância e outras informações.

names(ex01.av)
ex01.av$coef

ex01.av$res
residuals(ex01.av)

Após realizar a ANOVA, é necessário verificar os pressupostos do modelo:

Análise de resíduos

Homocedasticidade:

Graficamente, podemos analisar a homocedasticidade através de um box-plot,

boxplot(ex01.av$res ~ trat,ylab="Resíduos",xlab="Linhagens")

Através de um gráfico dos resíduos vs tratamentos,

plot.default(trat,ex01.av$res,ylab="Resíduos",xlab="Linhagens")

Ainda, pode-se avaliar através de um teste, como por exemplo o teste de Bartlett:

bartlett.test(ex01.av$res, trat)

Normalidade:

Graficamente, pode-se avaliar a normalidade dos resíduos fazendo

hist(ex01.av$res, main=NULL)
title("Histograma dos Resíduos")

stem(ex01.av$res)

qqnorm(ex01.av$res,ylab="Resíduos", main=NULL)
qqline(ex01.av$res)
title("Grafico Normal de Probabilidade dos Resíduos")

Através do teste de Shapiro-Wilk:

Teste de Shapiro-Wilk para Normalidade

Estatística do Teste

O objetivo deste teste é fornecer uma estatística de teste para avaliar se uma amostra tem distribuição Normal. O teste pode ser utilizado para amostras de qualquer tamanho.

A estatística W de teste para normalidade é definida como

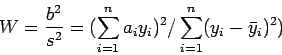$\begin{displaymath} W=\frac{b^2}{s^2}=(\sum\limits_{i=1}^na_iy_i)^2/\sum\limits_{i=1}^n(y_i-\bar{y}_i)^2) \end{displaymath}$

(1)

onde

é a variável aleatória observada e são coeficientes tabelados.

Execução do teste:

Par calcular a estatística W, de uma mostra aleatória de tamanho , dada por $y_1,y_2,\ldots,y_n$ , procede-se da seguinte forma:

Ordenar as observações em ordem decrescente: $y_1\le y_2\le \ldots \le y_n$ .
Calcular

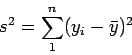
$\begin{displaymath} s^2=\sum\limits_1^n(y_i-\bar{y})^2 \end{displaymath}$
1. Se n é par, , faz-se
  
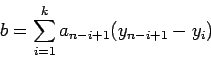
  $\begin{displaymath} b=\sum\limits_{i=1}^k a_{n-i+1}(y_{n-i+1}-y_i) \end{displaymath}$
  
  os valores de $a_{n-i+1}$ são tabelados.
2. Se é ímpar, , os cálculos permanecem os mesmos, exceto que, $a_{k+1}=0$
  
  $\begin{displaymath} b=a_n(y_n-y_1)+\ldots +a_({k+2}-y_k) \end{displaymath}$
Calcular

$\begin{displaymath} W=\frac{b^2}{s^2} \end{displaymath}$
Avaliar a estatística do teste através do P-valor. No caso de uma valor significativo para a estatística do teste, isso indica falta de normalidade para a variável aleatória analisada.

shapiro.test(ex01.av$res) #teste para normalidade

Independência:

A independência, com algumas restrições, pode ser analisada graficamente, através de

plot(ex01.av$fit, ex01.av$res, xlab="valores ajustados", ylab="resíduos")
title("resíduos vs Preditos")

Ainda é possível avaliar algum tipo de dependência através da ordenação dos resíduos, caso exista uma ordem de obte ção dos dados conhecida:

plot(ex01.av$fit, order(ex01.av$res), xlab="valores ajustados", ylab="resíduos")
title("resíduos vs Preditos")

Verificação de Outliers:

Utilizando o critério de +3 ou -3 desvios padronizados, pode-se avaliar a existência de candidatos à outlier utilizando os seguintes comandos:

plot(ex01.av) # pressione a tecla enter para mudar o gráfico

par(mfrow=c(2,2))
plot(ex01.av)
par(mfrow=c(1,1))

names(anova(ex01.av))
s2 <- anova(ex01.av)$Mean[2]   # estimativa da variância
  
res <- ex01.av$res           # extraindo resíduos
respad <- (res/sqrt(s2))  # resíduos padronizados 

boxplot(respad)
title("Resíduos Padronizados" )

plot.default(ex01$trat,respad, xlab="Linhagens")
title("Resíduos Padronizados" )

Teste de Tukey para comparações múltiplas

No R, o teste de Tukey é apresentado através de intervalos de confiança. A interpretação é: se o intervalo de confiança para a diferença entre duas médias não incluir o valor zero, siginifica que rejeita-se a hipótese nula, caso contrário, não rejeita-se.

O resultado pode ser visto através de uma tabela e/ou graficamente:

ex01.tu <- TukeyHSD(ex01.av)
ex01.tu
plot(ex01.tu)

Uma outra maneira é utilizar a seguinte função para estes dados.

## Diferença entre médias para um fator e igual número de repetições
#r=número de repetições
#t=número de tratamentos

dif.medias<-function(dados=ex01,r=6, t=9,alpha=0.95 )
{ attach(dados)
  modelo<-aov(resp~trat,data=dados)
  trat.m<-tapply(resp,trat,mean) 
  trat.m1<-trat.m 
  m1d<-outer(trat.m1,trat.m1,"-") 
  m1d<-m1d[lower.tri(m1d)] 
  m1n<-outer(names(trat.m1),names(trat.m1),paste,sep="-") 
  names(m1d)<-m1n[lower.tri(m1n)] 
  s2<-sum(resid(modelo)^2)/modelo$df.res 
  n<-r 
  dif.t<-qtukey(alpha,t,modelo$df.res)*sqrt(s2/n) 
  data.frame(dif=m1d,sig=ifelse(abs(m1d)>dif.t,"*","ns")) 
}

Contrastes

Em alguns casos, pode-se ter interesse em estudar contrastes específicos. No exemplo das linhagens, temos 9 tratamentos que possibilitam construir 8 contrastes ortogonais e independentes. Os contrastes poderiam ser:

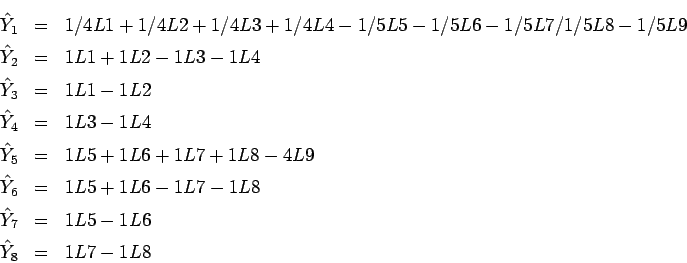
$\begin{eqnarray*} \hat{Y}_1 & = & 1/4L1 +1/4L2+1/4L3+1/4L4 -1/5L5-1/5L6-1/5L7/1... ...1L7-1L8\\ \hat{Y}_7 & = & 1L5-1L6\\ \hat{Y}_8 & = & 1L7-1L8 \end{eqnarray*}$

Pode-se obter a SQ de um contraste da seguinte maneira:

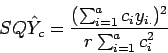
$\begin{displaymath} SQ\hat{Y}_c=\frac{(\sum_{i=1}^a c_iy_{i.})^2}{r\sum_{i=1}^ac_i^2} \end{displaymath}$

Os totais dos tratamentos são:

> tapply(ex01$resp,ex01$trat,sum)
  t1   t2   t3   t4   t5   t6   t7   t8   t9 
2272 2589 2078 1762 2051 2436  985 2423 2494

Por exemplo, a SQ para o contraste $\hat{Y}_1$ é dada da por:

$SQ\hat{Y}_1=\frac{(1/4*2272+1/4*2589+1/4*2078+1/4*1762-1/5*2051-1/5*2436-1/5*985-1/5*2423-1/5*2494)^2}{6*0.45}=3517,22$

Pode-se, contudo, inserir os contrastes dentro do quadro da ANOVA, informando ao R quais contrastes devem ser realizados. Para isso, deve-se definir uma matriz de contrastes.

> cont.ex01<-matrix(c(.25,.25,.25,.25,-.2,-.2,-.2,-.2,-.2,1,1,-1,-1,0,0,0,0,0,
  1,-1,0,0,0,0,0,0,0,0,0,1,-1,0,0,0,0,0,0,0,0,0,1,1,1,1,-4,0,0,0,0,1,1,-1,-1,
  0,0,0,0,0,1,-1,0,0,0,0,0,0,0,0,0,1,-1,0),nrow=9,ncol=8,byrow=F)

As colunas de cont.ex01 representam os contrastes que deverão ser realizados.

A função contrast() determina quais contrastes de tratamentos deverão ser considerados dentro da ANOVA.

> contrasts(ex01$trat)<-cont.ex01

Definidos os contrastes, faz-se a análise de variância

> ex01.av<-aov(resp~trat,data=ex01)

Em seguida, através da função summary.aov() faz-se o desdobramento dos graus de liberdade dos tratamentos para análise dos contrastes. Os números de 1 a 8 são as colunas da matriz de contrastes:

> summary.aov(ex01.av,split=list(trat=list(y1=1,y2=2,y3=3,y4=4,y5=5,y6=6,
  y7=7,y8=8)))

Veja quais os contrastes foram determinados pela função contrast().

> ex01.av$cont
$trat
    [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8]
t1  0.25    1    1    0    0    0    0    0
t2  0.25    1   -1    0    0    0    0    0
t3  0.25   -1    0    1    0    0    0    0
t4  0.25   -1    0   -1    0    0    0    0
t5 -0.20    0    0    0    1    1    1    0
t6 -0.20    0    0    0    1    1   -1    0
t7 -0.20    0    0    0    1   -1    0    1
t8 -0.20    0    0    0    1   -1    0   -1
t9 -0.20    0    0    0   -4    0    0    0

Exercícios

Analise o experimento da página 63 das notas de aula da disciplina de Planejamento de Experimentos I.
Clique aqui para ver e copiar o arquivo de dados.
Analise o experimento da página 64 das notas de aula da disciplina de Planejamento de Experimentos I.
Clique aqui para ver e copiar o arquivo de dados.

Opcional:

Nesta seção você poderá realizar a ANOVA usando operações aritméticas no R.

Utilize o arquivo de dados sobre linhagens como exemplo.

n <- length(resp)
n
nt <- length(levels(trat))
nt

correcao <- ((sum(resp))^2)/n
correcao

gltot <- n - 1
gltra <- nt - 1
glres <- n - nt

sqtot <- sum(resp^2) - correcao
sqtot

trtot <- tapply(resp, trat, sum)
sqtra <- (sum((trtot)^2))/6 - correcao
sqtra

sqres <- sqtot - sqtra
sqres

qmtra <- sqtra/gltra
qmres <- sqres/glres

fval <- qmtra/qmres
fval
pval <- pf(fval, gltra, glres, lower.tail = F)
pval

## Definindo o quadro da ANOVA

qav <- matrix(NA, nr=3, nc=5)
dimnames(qav) <- list(c("Tratamentos", "Residuo", "Total"),
c("GL","SQ","QM","valorF","valorP"))
qav

## Montando o Quadro da ANOVA

qav[1,] <- c(gltra, glres, qmtra, fval, pval)
qav[2,1:3] <- c(sqtra, sqres, qmres)
qav[3,1:2] <- c(gltot, sqtot)
qav

Simulação de um experimento

Uma indústria precisa decidir qual produto será utilizado para formulação de um detergente. Na composição, um ácido faz parte da fórmula. Esse ácido precisa ser dissolvido em água para ser misturado à fórmula do detergente. Quatro produtos estão sendo avaliados.

É importante nesse experimento que a dissolução do ácido seja rápida para que o processo de fabricação seja eficiente.

Simulação:

Utilizando comprimidos efervescentes para simular os ácidos, será realizado um experimento.

Quatro tipos(marcas) de comprimidos serão utilizados.

Em cada experimento serão realizadas 3 repetições em um delineamento completamente casualizado.

Deverão ser formados dois grupos para realizarem o experimento. Cada grupo receberá uma amostra extra para realizar um experimento piloto.

A variável resposta de interesse é o tempo de dissolução do comprimido por completo.

Obtenha os dados e faça a análise estatística.

Bom trabalho!

Adilson dos Anjos 2006-04-17