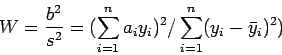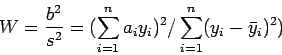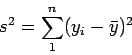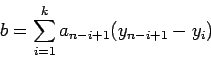Next: Teste de Tukey para
Up: Aula 02: Delineamento Completamente
Previous: Análise de resíduos
Estatística do Teste
O objetivo deste teste é fornecer uma estatística de teste para avaliar se uma amostra tem distribuição Normal. O teste pode ser utilizado para amostras de qualquer tamanho.
A estatística W de teste para normalidade é definida como
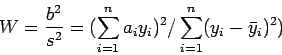 |
(1) |
onde
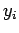 é a variável aleatória observada e
é a variável aleatória observada e 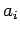 são coeficientes tabelados.
Execução do teste:
Par calcular a estatística W, de uma mostra aleatória de tamanho
são coeficientes tabelados.
Execução do teste:
Par calcular a estatística W, de uma mostra aleatória de tamanho 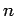 , dada por
, dada por
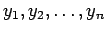 , procede-se da seguinte forma:
, procede-se da seguinte forma:
- Ordenar as observações em ordem decrescente:
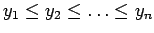 .
.
- Calcular
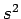
- Se n é par,
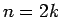 , faz-se
, faz-se
os valores de 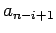 são tabelados.
são tabelados.
- Se
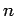 é ímpar,
é ímpar, 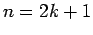 , os cálculos permanecem os mesmos, exceto que,
, os cálculos permanecem os mesmos, exceto que, 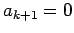
- Calcular
- Avaliar a estatística do teste através do P-valor. No caso de uma valor significativo para a estatística do teste, isso indica falta de normalidade para a variável aleatória analisada.
shapiro.test(ex01.av$res) #teste para normalidade
Independência:
A independência, com algumas restrições, pode ser analisada graficamente, através de
plot(ex01.av$fit, ex01.av$res, xlab="valores ajustados", ylab="resíduos")
title("resíduos vs Preditos")
Ainda é possível avaliar algum tipo de dependência através da ordenação dos resíduos, caso exista uma ordem de obte ção dos dados conhecida:
plot(ex01.av$fit, order(ex01.av$res), xlab="valores ajustados", ylab="resíduos")
title("resíduos vs Preditos")
Verificação de Outliers:
Utilizando o critério de +3 ou -3 desvios padronizados, pode-se avaliar a existência de candidatos à outlier utilizando os seguintes comandos:
plot(ex01.av) # pressione a tecla enter para mudar o gráfico
par(mfrow=c(2,2))
plot(ex01.av)
par(mfrow=c(1,1))
names(anova(ex01.av))
s2 <- anova(ex01.av)$Mean[2] # estimativa da variância
res <- ex01.av$res # extraindo resíduos
respad <- (res/sqrt(s2)) # resíduos padronizados
boxplot(respad)
title("Resíduos Padronizados" )
plot.default(ex01$trat,respad, xlab="Linhagens")
title("Resíduos Padronizados" )



Next: Teste de Tukey para
Up: Aula 02: Delineamento Completamente
Previous: Análise de resíduos
ADILSON DOS ANJOS
2005-04-15