3 Uso do pacote ltm
O pacote ltm é um dos mais completos dentro do R para uso com TRI.
Nesse capítulo serão utilizadas algumas funções para modelos de TRI.
Utilizaremos o conjunto de dados LSAT (Law School Admission Test, Bock e Lieberman
(1970)) disponível dentro do pacote ltm:
Inicialmente, pode-se explorar os dados com a função descript():
Descriptive statistics for the 'LSAT' data-set
Sample:
5 items and 1000 sample units; 0 missing values
Proportions for each level of response:
0 1 logit
Item 1 0.076 0.924 2.4980
Item 2 0.291 0.709 0.8905
Item 3 0.447 0.553 0.2128
Item 4 0.237 0.763 1.1692
Item 5 0.130 0.870 1.9010
Frequencies of total scores:
0 1 2 3 4 5
Freq 3 20 85 237 357 298
Point Biserial correlation with Total Score:
Included Excluded
Item 1 0.3618 0.1128
Item 2 0.5665 0.1531
Item 3 0.6181 0.1727
Item 4 0.5342 0.1444
Item 5 0.4351 0.1215
Cronbach's alpha:
value
All Items 0.2950
Excluding Item 1 0.2754
Excluding Item 2 0.2376
Excluding Item 3 0.2168
Excluding Item 4 0.2459
Excluding Item 5 0.2663
Pairwise Associations:
Item i Item j p.value
1 1 5 0.565
2 1 4 0.208
3 3 5 0.113
4 2 4 0.059
5 1 2 0.028
6 2 5 0.009
7 1 3 0.003
8 4 5 0.002
9 3 4 7e-04
10 2 3 4e-04
No resultado da função descript é fornecida a proporçã ode respostas para cada item,
a frequência de escores, a correlação bisserial e uma estatística χ2 para associações pareadas
entre os cinco items. Segundo Dimitris (2006), associações não significativas podem indicar
itens problemáticos.
3.1 Ajuste do modelo de Rasch
A função rasch() do pacote ltm estima o parâmetro de discriminação. Para definir o
parâmetro de discriminação como sendo 1, deve-se utilizar o argumento constraint.
Esse argumento deve ser fornecido na forma de uma matriz. Assim, para p itens o número
p + 1 indica o parâmetro de discriminação. Assim, constraint=cbind(length(LSAT)+1,1)
indica que o parâmetro p + 1, que corresponde ao parâmetro de discriminação, dve ser
1.
> fit1<-rasch(LSAT,constraint=cbind(length(LSAT)+1,1))
Para ver o resultado:
Call:
rasch(data = LSAT, constraint = cbind(length(LSAT) + 1, 1))
Model Summary:
log.Lik AIC BIC
-2473.054 4956.108 4980.646
Coefficients:
value std.err z.vals
Dffclt.Item 1 -2.8720 0.1287 -22.3066
Dffclt.Item 2 -1.0630 0.0821 -12.9458
Dffclt.Item 3 -0.2576 0.0766 -3.3635
Dffclt.Item 4 -1.3881 0.0865 -16.0478
Dffclt.Item 5 -2.2188 0.1048 -21.1660
Dscrmn 1.0000 NA NA
Integration:
method: Gauss-Hermite
quadrature points: 21
Optimization:
Convergence: 0
max(|grad|): 6.3e-05
quasi-Newton: BFGS
Uma outra maneira de se obter as estimativas dos parâmetros é:
> coef(fit1,prob=TRUE, order=TRUE)
Dffclt Dscrmn P(x=1|z=0)
Item 1 -2.8719712 1 0.9464434
Item 5 -2.2187785 1 0.9019232
Item 4 -1.3880588 1 0.8002822
Item 2 -1.0630294 1 0.7432690
Item 3 -0.2576109 1 0.5640489
Sem o argumento constraint, a função estima o parâmetro de discriminação.
> fit2<-rasch(LSAT)
> summary(fit2)
Call:
rasch(data = LSAT)
Model Summary:
log.Lik AIC BIC
-2466.938 4945.875 4975.322
Coefficients:
value std.err z.vals
Dffclt.Item 1 -3.6153 0.3266 -11.0680
Dffclt.Item 2 -1.3224 0.1422 -9.3009
Dffclt.Item 3 -0.3176 0.0977 -3.2518
Dffclt.Item 4 -1.7301 0.1691 -10.2290
Dffclt.Item 5 -2.7802 0.2510 -11.0743
Dscrmn 0.7551 0.0694 10.8757
Integration:
method: Gauss-Hermite
quadrature points: 21
Optimization:
Convergence: 0
max(|grad|): 2.5e-05
quasi-Newton: BFGS
OBS: utilizar ANOVA para comparar modelos.
Os valores de 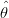 podem ser obtidos com a função factor.scores():
podem ser obtidos com a função factor.scores():
> factor.scores(fit2,met="EAP")
Call:
rasch(data = LSAT)
Scoring Method: Expected A Posteriori
Factor-Scores for observed response patterns:
Item 1 Item 2 Item 3 Item 4 Item 5 Obs Exp z1
1 0 0 0 0 0 3 2.364 -1.910
2 0 0 0 0 1 6 5.468 -1.429
3 0 0 0 1 0 2 2.474 -1.429
4 0 0 0 1 1 11 8.249 -0.941
5 0 0 1 0 0 1 0.852 -1.429
6 0 0 1 0 1 1 2.839 -0.941
7 0 0 1 1 0 3 1.285 -0.941
8 0 0 1 1 1 4 6.222 -0.439
9 0 1 0 0 0 1 1.819 -1.429
10 0 1 0 0 1 8 6.063 -0.941
11 0 1 0 1 1 16 13.288 -0.439
12 0 1 1 0 1 3 4.574 -0.439
13 0 1 1 1 0 2 2.070 -0.439
14 0 1 1 1 1 15 14.749 0.084
15 1 0 0 0 0 10 10.273 -1.429
16 1 0 0 0 1 29 34.249 -0.941
17 1 0 0 1 0 14 15.498 -0.941
18 1 0 0 1 1 81 75.060 -0.439
19 1 0 1 0 0 3 5.334 -0.941
20 1 0 1 0 1 28 25.834 -0.439
21 1 0 1 1 0 15 11.690 -0.439
22 1 0 1 1 1 80 83.310 0.084
23 1 1 0 0 0 16 11.391 -0.941
24 1 1 0 0 1 56 55.171 -0.439
25 1 1 0 1 0 21 24.965 -0.439
26 1 1 0 1 1 173 177.918 0.084
27 1 1 1 0 0 11 8.592 -0.439
28 1 1 1 0 1 61 61.235 0.084
29 1 1 1 1 0 28 27.709 0.084
30 1 1 1 1 1 298 295.767 0.632
se.z1
1 0.797
2 0.800
3 0.800
4 0.809
5 0.800
6 0.809
7 0.809
8 0.823
9 0.800
10 0.809
11 0.823
12 0.823
13 0.823
14 0.841
15 0.800
16 0.809
17 0.809
18 0.823
19 0.809
20 0.823
21 0.823
22 0.841
23 0.809
24 0.823
25 0.823
26 0.841
27 0.823
28 0.841
29 0.841
30 0.864
Após a calibração, pode-se utilizar um padrão de respostas qualquer para estimar a
habilidade. Basta fornecer o padrão de repostas da seguinte forma:
> factor.scores(fit2, resp.patterns = rbind(c(1,0,1,0,1), c(NA,1,0,NA,1)))
Call:
rasch(data = LSAT)
Scoring Method: Empirical Bayes
Factor-Scores for specified response patterns:
Item 1 Item 2 Item 3 Item 4 Item 5 Obs Exp z1
1 1 0 1 0 1 28 25.834 -0.466
2 NA 1 0 NA 1 0 252.440 -0.104
se.z1
1 0.816
2 0.871
3.2 Ajuste do modelo com dois parâmetros
O ajuste do modelo com dois parâmetro pode ser obtido com a função ltm().
Essa função pode ser especificada como uma fórmula onde o lado esquerdo deve conter
os dados e do lado direito a variável latente z1:
OBS: utilizar ANOVA para comparar modelos.
3.3 Ajuste do modelo com três parâmetros
Para ajustar um modelo com 3 parâmetros utiliza-se a função tpm)).
Será utilizado o conjunto de dados ’saresp manha’ para estimar esse modelo
> manha.tpm<-tpm(manha,control=list(optimizer="nlminb"))
Os valores dos parâmetros estimados foram:
Call:
tpm(data = manha, control = list(optimizer = "nlminb"))
Coefficients:
Gussng Dffclt Dscrmn
i1 0.243 1.979 0.632
i2 0.191 0.254 1.896
i3 0.156 1.114 1.717
i4 0.140 0.246 1.078
i5 0.024 -2.761 0.935
i6 0.025 -0.463 0.562
i7 0.098 0.786 0.812
i8 0.000 1.344 0.519
i9 0.175 1.043 1.520
i10 0.308 1.292 1.463
i11 0.005 -0.659 0.600
i12 0.323 0.972 0.771
i13 0.040 -0.104 1.169
i14 0.244 0.236 1.230
i15 0.265 2.298 1.741
i16 0.158 1.709 1.605
i17 0.493 0.798 2.322
i18 0.732 0.003 3.155
i19 0.076 0.434 0.956
i20 0.591 0.532 1.322
i21 0.000 0.975 0.581
i22 0.172 2.199 2.803
i23 0.215 2.352 2.245
i24 0.400 2.588 0.787
i25 0.002 0.996 0.959
i26 0.193 -0.244 1.362
i27 0.578 0.604 1.985
i28 0.067 0.361 1.518
i29 0.000 -1.089 1.219
i30 0.427 -0.616 1.365
Log.Lik: -17784.91
Os valores de θ podem ser obtidos com a função factor.scores() aplicada sobre o
objeto da classe tpm que contém as estimativas dos parâmetros do modelo.
> manha.prof<-factor.scores(manha.tpm)
Os valores de theta estimados são:
i1 i2 i3 i4 i5 i6 i7 i8 i9 i10 i11 i12 i13 i14 i15 i16
1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
2 0 0 0 0 0 0 0 0 0 0 0 1 0 1 1 0
3 0 0 0 0 0 0 0 0 0 1 0 0 0 0 1 0
4 0 0 0 0 0 0 0 0 1 1 0 0 0 0 1 0
5 0 0 0 0 0 0 0 1 0 0 0 1 0 1 0 0
6 0 0 0 0 0 0 0 1 0 1 0 0 0 0 1 0
i17 i18 i19 i20 i21 i22 i23 i24 i25 i26 i27 i28 i29 i30
1 1 1 0 1 0 0 0 1 0 0 1 1 1 1
2 0 1 0 1 0 0 0 1 0 0 1 0 0 1
3 0 0 0 0 0 1 1 0 0 0 1 1 0 1
4 0 1 0 0 1 0 1 0 0 1 1 0 0 1
5 0 1 0 0 0 0 1 0 1 0 0 0 1 1
6 0 1 0 1 0 0 0 0 0 0 0 1 1 0
Obs Exp z1 se.z1
1 1 0 -1.254365 0.6110829
2 1 0 -1.800145 0.6841814
3 1 0 -1.840739 0.6910352
4 1 0 -1.526407 0.6573003
5 1 0 -0.976459 0.5065874
6 1 0 -1.330498 0.5644371
3.4 Gráficos
No R a função plot() pode assumir um comportamento específico para cada tipo de
objeto.
Por exemplo, a função plot aplicada ao objeto fit2 produz a CCI.
ou
As curvas de informação do item podem ser obtidas da seguinte maneira:
A função de informação do teste pode ser obtida da seguinte maneira:
Um plot do objeto que contém a habilidade fornece um gráfico de densidade dessa
variável.
3.5 Exercício
Utilize o conjunto de dados ’saresp noturno’ e ajuste um modelo com 3 parâmetros.
3.6 Pacote irtoys
O pacote irtoys possui uma função chamada est() que possui características
similares ao software BILOG quanto as opções de estimação. Inclusive, é possível
utilizar as ferramentas de estimação do BILOG caso esse esteja instalado em seu
computador.
Nesse material, não será abordado o BILOG. Será utilizado o pacote ltm como
ferramenta de estimação dos parâmetros dos modelos de interesse.
Para mais informações sobre a função est() veja o arquivo de ajuda do pacote
(help(est)).
O ajuste de modelos com três parâmetros pode ser obtido da seguinte maneira:
> manha.par<-est(manha, model = "3PL", engine = "ltm", nqp = 20, est.distr = FALSE,
+ logistic = TRUE, nch = 5, a.prior = TRUE, b.prior = FALSE, c.prior = TRUE,
+ bilog.defaults = TRUE, rasch = FALSE, run.name = "meumodelo")
O objeto manha.par contém os valores dos parâmetros a, b e c do modelo com 3
parâmetros. Para visualizas os primeiros parâmetros digite:
[,1] [,2] [,3]
i1 0.6644912 1.9939205 0.25346762
i2 1.9176240 0.2600441 0.19425154
i3 1.7516722 1.1147812 0.15854534
i4 1.0914463 0.2583877 0.14447929
i5 0.9412978 -2.7227852 0.04245911
i6 0.5695324 -0.4206178 0.03557638
Para obter o θ ou a proficiência ou habilidade de cada indivíduo, após a estimação dos
parâmetros do modelo, pode-se utilizar a função eap(). É necessário fornecer o arquivo de
respostas e o objeto com os parêmetros estimados do modelo:
> manha.sco<-eap(manha,manha.par,qu=normal.qu())
O objeto manha.sco contém o vetor θ de cada indivíduo.
est sem n
[1,] 0.06110404 0.4771474 30
[2,] 0.58837056 0.4089677 30
[3,] 1.92623806 0.4680314 30
[4,] -1.71143568 0.6046441 30
[5,] -0.47840008 0.4540995 30
[6,] -0.29040561 0.4498074 30
Um objeto final, com os scores, identificação e posição dos respondentes pode ser
criado com os seguintes comandos:
> final.rank<-data.frame('id'=saresp$id,'turno'=saresp$turno,'score'=manha.sco[,1],'posição'=rank(manha.sco[,1]),'acertos'=margin.table(manha,1))
> head(final.rank)
id turno score posição acertos
1 11001138433 m07 0.06110404 538 16
2 11002964093 m07 0.58837056 748 17
3 11004154243 m07 1.92623806 987 26
4 11005367283 m07 -1.71143568 15 8
5 11007519633 m07 -0.47840008 326 12
6 11008054863 m07 -0.29040561 398 13
Pode-se visualizar o resultado ordenado pelo número de acertos,
> final.acertos<- final.rank[order(final.rank$acertos),]
> head(final.acertos)
id turno score posição acertos
25 21002457753 m07 -0.9453425 156 7
88 41044200343 m07 -1.9417899 2 7
128 71025145903 m07 -1.6560666 18 7
149 81024867083 m07 -1.5962607 24 7
183 91057432493 m07 -1.8380660 7 7
192 101006567063 m07 -1.6005866 23 7
id turno score posição acertos
422 281032975343 m07 2.450968 999 27
803 711010603953 m07 2.348995 997 27
859 761011075233 m07 2.177786 993 27
229 121035651183 m07 2.604056 1000 28
628 511003326933 m07 2.360057 998 28
558 441003142213 m07 2.766691 1001 29
> final.score<- final.rank[order(final.rank$score),]
> head(final.score)
id turno score posição acertos
257 131061868283 m07 -1.942270 1 7
88 41044200343 m07 -1.941790 2 7
971 861004925633 m07 -1.905838 3 7
315 191001523743 m07 -1.888097 4 8
325 201008250873 m07 -1.857824 5 10
395 261017778043 m07 -1.847286 6 7
id turno score posição acertos
409 271024133193 m07 2.335383 996 27
803 711010603953 m07 2.348995 997 27
628 511003326933 m07 2.360057 998 28
422 281032975343 m07 2.450968 999 27
229 121035651183 m07 2.604056 1000 28
558 441003142213 m07 2.766691 1001 29
Se for de interesse, pode-se alterar a escala do score com a função score.transform()
do pacote CTT. Por exemplo, pode-se mudar a escala N(0,1) para uma escala N(500,10):
> novo.score<-score.transform(manha.sco[,1], mu.new = 500, sd.new = 10, normalize = FALSE)
> head(novo.score$new,n=30)
[1] 500.6941 506.6993 521.9368 480.5060 494.5495 496.6906
[7] 496.1962 496.0810 491.9442 507.9800 504.4469 499.2399
[13] 504.9959 495.8971 492.5432 490.3022 513.9534 511.7711
[19] 520.0580 510.6101 501.2948 505.0943 506.0797 505.7781
[25] 489.2313 513.4319 503.0251 514.0883 487.8618 504.2727
Para obtenção da curva característica pode-se obter um plot do objeto que contém o
resultado da estimação dos parâmetros.
Call:
tpm(data = manha, control = list(optimizer = "nlminb"))
Model Summary:
log.Lik AIC BIC
-17784.91 35749.82 36191.61
Coefficients:
value std.err z.vals
Gussng.i1 0.2429 0.1601 1.5173
Gussng.i2 0.1914 0.0715 2.6755
Gussng.i3 0.1560 0.0396 3.9397
Gussng.i4 0.1398 0.1256 1.1126
Gussng.i5 0.0243 0.8273 0.0294
Gussng.i6 0.0251 NaN NaN
Gussng.i7 0.0982 0.1198 0.8192
Gussng.i8 0.0001 0.0065 0.0183
Gussng.i9 0.1748 0.0413 4.2321
Gussng.i10 0.3085 0.0486 6.3469
Gussng.i11 0.0049 0.1762 0.0278
Gussng.i12 0.3234 0.1220 2.6495
Gussng.i13 0.0400 NaN NaN
Gussng.i14 0.2438 0.0981 2.4849
Gussng.i15 0.2649 0.0281 9.4235
Gussng.i16 0.1577 0.0326 4.8373
Gussng.i17 0.4930 0.0404 12.2168
Gussng.i18 0.7319 0.0414 17.6636
Gussng.i19 0.0756 0.1514 0.4992
Gussng.i20 0.5913 0.0759 7.7905
Gussng.i21 0.0001 0.0073 0.0160
Gussng.i22 0.1724 0.0166 10.3866
Gussng.i23 0.2147 0.0178 12.0598
Gussng.i24 0.4004 0.0700 5.7213
Gussng.i25 0.0015 0.0620 0.0242
Gussng.i26 0.1934 0.1306 1.4811
Gussng.i27 0.5778 0.0505 11.4507
Gussng.i28 0.0670 0.0554 1.2108
Gussng.i29 0.0002 0.0133 0.0180
Gussng.i30 0.4272 0.1537 2.7800
Dffclt.i1 1.9792 0.5517 3.5877
Dffclt.i2 0.2536 0.1613 1.5723
Dffclt.i3 1.1143 0.1128 9.8832
Dffclt.i4 0.2461 0.3465 0.7103
Dffclt.i5 -2.7609 1.4287 -1.9324
Dffclt.i6 -0.4627 NaN NaN
Dffclt.i7 0.7861 0.3722 2.1121
Dffclt.i8 1.3443 0.2382 5.6444
Dffclt.i9 1.0433 0.1260 8.2807
Dffclt.i10 1.2917 0.1692 7.6354
Dffclt.i11 -0.6594 0.6338 -1.0405
Dffclt.i12 0.9722 0.5143 1.8905
Dffclt.i13 -0.1045 NaN NaN
Dffclt.i14 0.2355 0.2848 0.8269
Dffclt.i15 2.2984 0.3702 6.2085
Dffclt.i16 1.7088 0.1657 10.3109
Dffclt.i17 0.7982 0.1462 5.4585
Dffclt.i18 0.0034 0.2019 0.0170
Dffclt.i19 0.4344 0.4160 1.0443
Dffclt.i20 0.5322 0.3892 1.3672
Dffclt.i21 0.9748 0.1749 5.5718
Dffclt.i22 2.1989 0.2248 9.7807
Dffclt.i23 2.3523 0.3034 7.7525
Dffclt.i24 2.5881 0.7172 3.6086
Dffclt.i25 0.9957 0.1644 6.0548
Dffclt.i26 -0.2439 0.3168 -0.7699
Dffclt.i27 0.6040 0.2160 2.7956
Dffclt.i28 0.3611 0.1299 2.7800
Dffclt.i29 -1.0891 0.1077 -10.1158
Dffclt.i30 -0.6164 0.4812 -1.2809
Dscrmn.i1 0.6319 0.4368 1.4468
Dscrmn.i2 1.8956 0.4190 4.5241
Dscrmn.i3 1.7169 0.4210 4.0781
Dscrmn.i4 1.0778 0.2710 3.9764
Dscrmn.i5 0.9354 0.2044 4.5769
Dscrmn.i6 0.5622 NaN NaN
Dscrmn.i7 0.8122 0.2363 3.4365
Dscrmn.i8 0.5186 0.0843 6.1488
Dscrmn.i9 1.5202 0.3262 4.6604
Dscrmn.i10 1.4633 0.4762 3.0728
Dscrmn.i11 0.5996 0.1182 5.0711
Dscrmn.i12 0.7714 0.3154 2.4456
Dscrmn.i13 1.1690 NaN NaN
Dscrmn.i14 1.2303 0.2896 4.2484
Dscrmn.i15 1.7405 0.9728 1.7892
Dscrmn.i16 1.6050 0.5065 3.1688
Dscrmn.i17 2.3217 0.7876 2.9476
Dscrmn.i18 3.1551 1.1588 2.7228
Dscrmn.i19 0.9562 0.2872 3.3297
Dscrmn.i20 1.3218 0.5227 2.5289
Dscrmn.i21 0.5815 0.0856 6.7911
Dscrmn.i22 2.8027 1.3812 2.0292
Dscrmn.i23 2.2450 0.9678 2.3197
Dscrmn.i24 0.7867 0.5440 1.4460
Dscrmn.i25 0.9592 0.2003 4.7884
Dscrmn.i26 1.3621 0.2909 4.6830
Dscrmn.i27 1.9852 0.7067 2.8091
Dscrmn.i28 1.5183 0.2473 6.1397
Dscrmn.i29 1.2185 0.1310 9.2982
Dscrmn.i30 1.3646 0.3426 3.9827
Integration:
method: Gauss-Hermite
quadrature points: 21
Optimization:
Optimizer: nlminb
Convergence: 0
max(|grad|): 0.012
A estimativa da proficiência de cada indivíduo pode ser obtida com a função
factor.scores():
> manha.prof<-factor.scores(manha.tpm)
> head(manha.prof$score)
i1 i2 i3 i4 i5 i6 i7 i8 i9 i10 i11 i12 i13 i14 i15 i16
1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
2 0 0 0 0 0 0 0 0 0 0 0 1 0 1 1 0
3 0 0 0 0 0 0 0 0 0 1 0 0 0 0 1 0
4 0 0 0 0 0 0 0 0 1 1 0 0 0 0 1 0
5 0 0 0 0 0 0 0 1 0 0 0 1 0 1 0 0
6 0 0 0 0 0 0 0 1 0 1 0 0 0 0 1 0
i17 i18 i19 i20 i21 i22 i23 i24 i25 i26 i27 i28 i29 i30
1 1 1 0 1 0 0 0 1 0 0 1 1 1 1
2 0 1 0 1 0 0 0 1 0 0 1 0 0 1
3 0 0 0 0 0 1 1 0 0 0 1 1 0 1
4 0 1 0 0 1 0 1 0 0 1 1 0 0 1
5 0 1 0 0 0 0 1 0 1 0 0 0 1 1
6 0 1 0 1 0 0 0 0 0 0 0 1 1 0
Obs Exp z1 se.z1
1 1 0 -1.254365 0.6110829
2 1 0 -1.800145 0.6841814
3 1 0 -1.840739 0.6910352
4 1 0 -1.526407 0.6573003
5 1 0 -0.976459 0.5065874
6 1 0 -1.330498 0.5644371
[1] "score.dat" "method" "B" "call"
[5] "resp.pats" "coef"
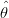 podem ser obtidos com a função factor.scores():
podem ser obtidos com a função factor.scores():
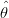 podem ser obtidos com a função factor.scores():
podem ser obtidos com a função factor.scores():