24 Métodos para descrever a variação

Objetivo

O objetivo desta seção é apresentar métodos para descrever a variação de dados. Existem muitas alternativas para o estudo da variabilidade de dados. Além de gráficos e medidas como variância e desvio padrão, podem ser aplicados testes para comparação de variâncias, por exemplo.

Arquivo de dados

Ainda os dados sobre tempo de parada da linha de produção.

Em particular, será estudado o código 31 nesse capítulo

> cod.31<-subset(linha,cod==31,select=c(names(linha)));cod.31

Avaliação gráfica da variação

Um gráfico de ramo-e-folhas:

> stem(cod.31$tempo,scale=2)

  The decimal point is 1 digit(s) to the right of the |

   0 | 11222222333333444455566666677777889999
   1 | 00000001222223334444455556667778888
   2 | 00000011122333344455566788999
   3 | 00223378
   4 | 0133445677789
   5 | 2377778
   6 | 0124578
   7 | 134467
   8 | 9
   9 | 7
  10 | 3
  11 | 55
  12 | 4
  13 | 
  14 | 
  15 | 0
  16 | 13
  17 | 3
  18 | 
  19 | 8
  20 | 
  21 | 
  22 | 
  23 | 9
  24 | 
  25 | 9

Observe que, a distribuição é bastante assimétrica. Existem muitas paradas com até uma hora de duração e poucas com mais de uma hora de duração.

Um histograma:

> hist(cod.31$tempo,nclass=10,col=rainbow(13))

Se for de interesse, pode-se traçar a linha de densidade dos dados.

> hist(cod.31$tempo,prob=T,nclass=10,ylim=c(0,0.035))  
> lines(density(cod.31$tempo) ) # insere a linha
> rug(cod.31$tempo) # insere uma barra com freq. de pontos

Um box-plot:

> boxplot(cod.31$tempo)

A função boxplot.stats() fornece informações sobre dados do box plot. Especificamente, $out mostra as observações que podem ser consideradas candidatos a outlier (dados discrepantes).

> boxplot.stats(cod.31$tempo)
$stats
[1]  1.0 10.0 20.0 45.5 97.0

$n
[1] 156

$conf
[1] 15.50921 24.49079

$out
 [1] 198 163 115 103 124 239 161 173 115 259 150

Dados discrepantes podem fornecer muita informação. Por exemplo, o tempo de parada registrado para esse código, pode estar tendo outras causas que levam a esses valores discrepantes. Obviamente, é necessário checar se esses dados foram obtidos de forma correta.

Algumas medidas de variação

Além de gráficos, existem várias medidas para analisar a variabilidade.

1. Variância

   A variância, definida por 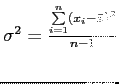$\sigma^2=\frac{\sum\limits_{i=1}^n(x_i-\bar{x})^2}{n-1}$, pode ser obtida com o comando var():

   > var(tempo)
   [1] 2616.395
   

   > tapply(tempo,cod,var)
              1            2            5            6            7            8 
    2557.476190    32.000000 50922.800000  2377.659960 35942.916667   646.598227 
              9           31           32           33           34           35 
   28084.500000  1866.541398  1800.000000   151.439545   174.078431    12.370630 
             36           38           41           43           44           81 
     303.000000     6.982143  2192.457319  7910.650000   174.500000  3326.000000 
             82           84          321          322          421 
      14.596639     6.200000     2.000000   818.719080    47.233766
   

2. Desvio padrão

   O desvio padrão, definido como $\sigma=\sqrt{s^2}$ pode ser obtido com o comando sd:

   > sd(tempo)
   [1] 51.1507
   

   > tapply(tempo,cod,sd)
            1          2          5          6          7          8          9 
    50.571496   5.656854 225.660807  48.761255 189.586172  25.428296 167.584307 
           31         32         33         34         35         36         38 
    43.203488  42.426407  12.306078  13.193879   3.517191  17.406895   2.642374 
           41         43         44         81         82         84        321 
    46.823683  88.941835  13.209845  57.671483   3.820555   2.489980   1.414214 
          322        421 
    28.613268   6.872683
   

3. Coeficiente de variação

   O coeficiente de variação, definido como $CV \%=\frac{s}{\bar{x}}100$, pode ser utilizado para avaliar a variabilidade dos dados. Em geral, é útil para comparar medidas semelhantes.

   > cod.31<-subset(linha,cod==31,select=c(names(linha)));cod.31
   > cod.34<-subset(linha,cod==34,select=c(names(linha)));cod.34
   > cv.31<-(sd(cod.31$tempo)/mean(cod.31$tempo))*100;cv.31
   [1] 123.1453
   > cv.34<-(sd(cod.34$tempo)/mean(cod.34$tempo))*100;cv.34
   [1] 84.21625
   

   Nesse exemplo, existe uma maior precisão na variável tempo 34 em relação ao código 31.

Testes sobre variâncias

Além de estatísticas descritivas, pode-se realizar testes de hipóteses para estudar as variâncias.

Por exemplo, pode ser de interesse testar variâncias com uma valor de referência ou ou comparar variâncias entre processos.

No primeiro caso, pode-se utilizar um teste de qui-quadrado para testar a hipótese

$$H_0: \sigma^2=\sigma^2_R$$

$$H_1: \sigma^2\neq \sigma^2_R$$

$\sigma^2_R$ é o valor da variância referencial.

A estatística de teste é dada por $\chi^2=\frac{(n-1)s^2}{\sigma^2_R}$

Como exemplo, pode-se ter interesse em comparar a variância do código 1 em relação a variância total da variável tempo.

> var(tempo)
[1] 2616.395

> var(tempo[cod==1])
[1] 2557.476

Utilizando o teste de qui-quadrado,

> var(tempo)
[1] 2616.395
> var(tempo[cod==1])
[1] 2557.476
> length(tempo[cod==1])
[1] 7

> qui<-((length(tempo[cod==1])-1)*var(tempo[cod==1]))/var(tempo);qui
[1] 5.864887

> qchisq(.95,length(tempo[cod==1])-1)
[1] 12.59159

> 1-pchisq(qui,length(tempo[cod==1])-1)
[1] 0.4384947

Neste exemplo, não rejeita-se a hipótese nula, ou seja, não há diferença significativa entre a variância do código 1 em relação a variância total.

Se for de interesse testar a hipótese

$$H_0: \sigma^2_1=\sigma^2_2$$

$$H_1: \sigma^2_1\neq \sigma^2_2$$

pode-se utilizar a estatística de teste baseada na razão de variâncias,

$$F=\frac{\hat{\sigma}^2_1}{\hat{\sigma}^2_2}$$

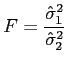
Por exemplo, pode-se ter interesse comparar as variâncias do código 1 e do código 31.

> var.test(tempo[cod==1],tempo[cod==31])

	F test to compare two variances

data:  tempo[cod == 1] and tempo[cod == 31] 
F = 1.3702, num df = 6, denom df = 155, p-value = 0.4599
alternative hypothesis: true ratio of variances is not equal to 1 
95 percent confidence interval:
 0.5500939 6.7029025 
sample estimates:
ratio of variances 
          1.370168

Portanto, não rejeita-se a hipótese nula, ou seja, não há evidências para considerar que as variâncias dessas duas amostras diferem.

Exercícios

1. Construa um boxplot para cada um dos códigos de parada. Analise a variabilidade.
2. Escolha um outro código de parada e compare com os resultados estudados nessa seção. Utilize as medidas de variação apresentadas, além da análise gráfica;
3. Estude o comportamento de variação dos turnos de produção. Compare os turnos entre si com relação à variação;