31 Amostragem por aceitação

Objetivos

O objetivo desta seção é encontrar a probabilidade de aceitação para uma amostradege por aceitação simples de lotes. Também será dado enfoque para a construção da CCO. Procure entender os comandos do R e interpretar os resultados.

Probabilidade de aceitação - Pa

Como visto na teoria, a probabilidade de aceitação de um lote - Pa - é dada pelo uso da expressão da Distribuição Binomial. Nesse caso, desejamos encontrar a $P(d\leq c)$.

$$P_A=P(d\leq c) =\sum\limits_{d=0}^c\frac{n!}{d!(n-d)!}p^d(1-p)^{n-d}$$

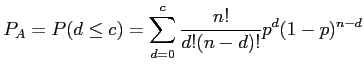
No R pode-se utilizar a distribuição Binomial, considerando o exemplo fornecido na teoria, da seguinte maneira:

> dbinom(0,89,0.01)+dbinom(1,89,0.01)+dbinom(2,89,0.01) 
[1] 0.93969
> sum(dbinom((0:2),89,0.01))
[1] 0.93969

Essa é a probabilidade de aceitação de um lote com $n=89$, $c=2$ e $p=0,01$.

Construção da CCO

De uma maneira geral, pode-se construir uma curva característica de operação e avaliar qual é o comportamento da probabilidade de aceitação Pa em função das características da amostragem e do lote.

Considerando que estamos tratando com a distribuição Binomial, pode-se construir uma curva considerando diferentes proporções de defeituosos em um lote, para um determinado valor de $n$ e $c$.

De forma semelhante a realizada anteriormente, pode-se construir uma função da seguinte maneira:

> cco.s<-function(n=89,c=2){
   p.x<-seq(0,0.08,length=100)
   pa.y<-seq(0,1,length=100)
   p <-numeric()
   plot(p.x,pa.y,type="n",xlab="Proporção de defeituosos - p",
   ylab="Probabilidade de aceitação - Pa",cex.lab=1.5)
   abline(h=0)
           for(i in 1:length(p.x))
          {
           p[i]<-sum(dbinom((0:c),n,p.x[i]))
           
          }
     lines(p.x,p)
    text(c(0.05,0.047,0.05,0.047),c(0.6,0.6,0.5,0.5),
    c("n"=n,'n =',"c"=c,'c ='),cex=1.3)
    }

Para utilizar a função cco.s() deve-se fornecer o tamanho da amostra e o valor de $c$.

Construída a curva, podemos, então, encontrar qual o valor de $Pa$ para um determinado valor de p. Como exemplo, se o valor de $p=0,02$, para encontrar $Pa$, pode-se desenhar um linha vertical

> cco.s()
> abline(v=0.02,col='red',lty=2)  # ou
> segments(0.02,0,0.02,0.99, col= 'blue',lty=2)

Para encontrar o valor de $Pa$, usa-se a função locator(). Utilize a função da seguinte maneira:

1. faça o gráfico e mantenha a janela gráfica aberta aberta;
2. na linha de comando do Rutilize a função para localizar $n=1$ ponto:

   > locator(n=1,type="p",col='red')
   

3. vá para a janela gráfica e clique no ponto onde a linha vertical cruza a curva;
4. volte para a linha de comando do Re observe o valor de $y$.

Exercícios

1. Defina as condições de amostragem de um lote (n, p, c). Encontre o valor de $Pa$;
2. Suponha uma situação factível (por exemplo, no seu local de trabalho, um exemplo de livro ou mesmo hipotético). Defina o valor de p e/ou c. Tente encontrar um tamanho de amostra $n$ para essa condição.