29 Gráficos de controle: tamanho de amostra

Objetivos

O objetivo dessa seção é encontrar o erro $\beta$ para alguns gráficos de controle para variáveis e atributos e construir a curva característica de operação (CCO).

Valor de $\beta$ e CCO para o gráfico $\bar{x}$.

O valor de $\beta$ para o gráfico $\bar{x}$ depende da constante $L$, que é o número de desvios para os limites de controle, do valor de $k$, que é a constante a ser avaliada, ou seja, e é ela quem determina qual a chance de um ponto ultrapassar esse limite em função do desvio padrão e $n$ é o tamanho da amostra utilizada.

Nesse exemplo, vamos utilizar o valor padrão de $L=3$, assumindo $k=2$ e um tamanho de amostra $n=6$. A função beta.xbar calcula o valor de $\beta$ nessas condições.

> beta.xbar<-function(L=3,k=2,n=6)
               {
  phi.1= (L-k*sqrt(n))
  phi.2= (-L-k*sqrt(n))   
  beta<-pnorm(phi.1)- pnorm(phi.2) 
  result<-round(c(beta,phi.1,phi.2),4)
  nomes<-c("beta","phi.1","phi.2")
  names(result)<-nomes
  print(result)
}

Agora, basta utilizá-la:

> beta.xbar()
   beta   phi.1   phi.2 
 0.0288 -1.8990 -7.8990

O valor de 0.0288 é o risco de que uma mudança na ordem de $2\sigma$ não seja percebida no gráfico de controle.

Fazendo

$$CMP=\frac{1}{1-0.0288}= 1,029654$$

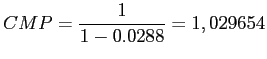
obtém-se o número de amostras necessárias para se detectar uma mudança na média na ordem de $2\sigma$.

De forma geral, pode-se construir uma CCO para esse tipo de gráfico. Nesse caso, é possível definir o tamanho de amostra em função do risco assumido e da definição da variação na média.

> cco.xbar<-function(n.min=2,n.max=4,L=3)
  {
   k.x<-seq(0,4.5,length=100)
   beta.y<-seq(0,1,length=100)
   phi.1<-numeric()
   phi.2<-numeric()
   beta <-numeric()
   plot(k.x,beta.y,type="n",xlab="k",ylab=expression(beta))
   abline(h=0)
   for(j in n.min:n.max)
   {
        for(i in 1:length(k.x))
          {
           phi.1[i]<- L-k.x[i]*sqrt(j)
           phi.2[i]<- -L-k.x[i]*sqrt(j)
          }
     beta<-pnorm(phi.1)-pnorm(phi.2)
     legend(3,.8,leg=n.min:n.max,lty=n.min:n.max,pch=20,cex=1.2,
     title="n",pt.cex=1.0,ncol=2,pt.lwd=1.3)   
     lines(k.x,beta,lty=j)
    }
}

Para identificar um ponto, e encontrar o tamanho de amostra, utilize a função points:

> points(1.0,.10,pch=4)

Valor de $\beta$ e CCO para o gráfico $p$.

Para o gráfico de controle p, pode-se, também, encontrar o valor de $\beta$. Nesse caso, a distribuição utilizada, é a distribuição Binomial.

Para criar essa função, devemos fornecer o tamanho da amostra e os limites de controle do gráfico, além do valor da linha central.

> beta.p<-function(n=50,p=0.3,LSC=0.3697,LIC=0.0303)
               {
  D1<- pbinom(n*LSC, n, p, lower.tail = TRUE, log.p = FALSE)
  D2<- pbinom(n*LIC, n, p, lower.tail = TRUE, log.p = FALSE)   
  beta<-D1-D2
  result<-round(c(beta,D1,D2),4)
  nomes<-c("beta","D1","D2")
  names(result)<-nomes
  print(result)
               }

> beta.p()
  beta     D1     D2 
0.8594 0.8594 0.0000

Nesse caso, se $p=0.3$ (um processo fora de controle), tem-se o valor de $\beta=0.8594$, ou seja, teremos um CMP=7, que indica o número médio de amostras para se identificar uma mudança dessa magnitude, através de um ponto fora de controle.

Para diminuir o valor de $\beta$, pode-se aumentar o tamanho da amostra e/ou diminuir o intervalo de obtenção das amostras. Ao invés de coletar uma amostra a cada hora (sriam necesárias 7 horas para encontrar o problema), poderia-se reduzir para meia hora, ou seja, teríamos um intervalo de 3,5 horas para encontrar o problema.

A curva característica de operação pode ser obtida com a seguine função:

> cco.p<-function(n=50,LSC=0.3697,LIC=0.0303)
  {
   p.x<-seq(0,.8,length=100)
   beta.y<-seq(0,1,length=100)
   D1<-numeric()
   D2<-numeric()
   beta <-numeric()
   plot(p.x,beta.y,type="n",xlab="p",ylab=expression(beta))
   abline(h=0)
           for(i in 1:length(p.x))
    	{
    	D1[i]<- pbinom(n*LSC, n, p.x[i])
    	D2[i]<- pbinom(n*LIC, n, p.x[i]) 
    	}
    beta<-D1-D2
    text(c(.5,.5,.5),c(.8,.75,.7),c("n"=n,LSC,LIC),adj=c(0,05))
    text(c(.48,.48,.48),c(.8,.75,.7),c('n=','LSC=','LIC='),adj=c(1,05))
    lines(p.x,beta)
    result<-list(beta,p.x)
    nomes<-c("beta","p")
    names(result)<-nomes
    return(result)
 }

A curva pode ser gerada com

> cco.p()

Observe que ela representa a curva apenas para os parâmetros fornecidos.

Valor de $\beta$ e CCO para o gráfico $c$.

Para o gráfico de controle c, utilizamos a distribuição Poisson para encontrar o valor de $\beta$:

> beta.c<-function(c=15,LSC=33.22,LIC=6.48)
               {
  D1<- ppois(LSC, c)
  D2<- ppois(LIC, c )   
  beta<-D1-D2
  result<-round(c(beta,D1,D2),4)
  nomes<-c("beta","D1","D2")
  names(result)<-nomes
  print(result)
               }

na função beta.c, devemos fornecer o parâmetro c (número de não-conformes) e os limites de controle. Como os limites necessitam ser números inteiros, o R automaticamente faz o arredondamento.

> beta.c()
  beta     D1     D2 
0.9924 1.0000 0.0076

Para c=15, teremos um $\beta=0,9924$.

Também, para o gráfico c, pode-se construir a CCO. Basta apenas fornecer os limites de controle:

> cco.c<-function(LSC=33.22,LIC=6.48)
  {
   c.x<-seq(0,49.5,by=.5)
   beta.y<-seq(0,1,length=100)
   D1<-numeric()
   D2<-numeric()
   beta <-numeric()
   plot(c.x,beta.y,type="n",xlab="c",ylab=expression(beta))
   abline(h=0)
           for(i in 1:length(c.x))
          {
           D1[i]<- ppois(LSC, c.x[i])
           D2[i]<- ppois(LIC, c.x[i]) 
          }
   beta<-D1-D2
   text(c(40,40),c(.85,.8),c(LSC,LIC),adj=c(0,05))
   text(c(40,40),c(.85,.8),c('LSC=','LIC='),adj=c(1,05))
   lines(c.x,beta)
   result<-list(beta,c.x)
   nomes<-c("beta","c")
   names(result)<-nomes
   return(result)
 }

Utilize, então a função cco.c(). Se for de interesse, pode-se encontrar um valor de $\beta$ para um determinado parâmetro $c$, fazendo:

> betas<-cco.c()
> names( betas)
> betas$beta[which(betas$c==49.5)] # por exemplo

Exercícios

1. Para os exemplos de gráficos de controle $\bar{x}$, $p$ e $c$ estudados no pacote qcc (exemplos: pistonrings, orangejuice2, circuit), determine a chance de se cometer o erro tipo II.